題目連結:
題目意譯:
現在有一個有向圖,其有著 n 個有色節點以及 m 條邊。這些節點編號為 0 到 n - 1。
你被給定一個字串 colors,其中 colors[i] 為一個小寫英文字母並代表著在這個圖中第 i 個節點的顏色(索引值從 0 開始)。你同時也被給定一個二維陣列 edges,其中 edges[j] = [aj, bj] 代表著有一條有向邊從節點 aj 指向節點 bj 。
在圖中的一條「合法路徑」為一個節點序列 x1 → x2 → x3 → …… → xk 使得對於每個 i,其中 1 ≦ i < k,都滿足有一條有向邊從 xi 指向 xi+1。這條路徑的「顏色值」定義為那些顏色為路徑上出現最頻繁的顏色之節點數量。
回傳給定的圖中所有合法路徑中最大的顏色值。如果圖中包含環,則回傳 -1。
限制:
n == colors.length
m == edges.length
1 ≦ n ≦ 10 ^ 5
0 ≦ m ≦ 10 ^ 5
colors 由小寫英文字母組成。
0 ≦ aj, bj < n
範例測資:
範例 1:
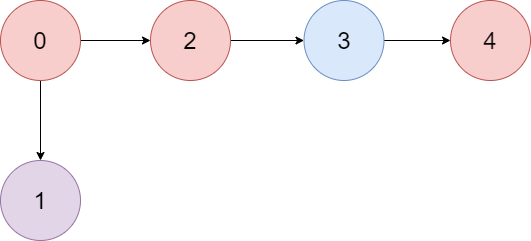
輸入: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
輸出: 3
解釋: 路徑 0 → 2 → 3 → 4 包含 3 個顏色為 "a" 的節點(上圖中的紅色)。
範例 2:
輸入: colors = "a", edges = [[0,0]]
輸出: -1
解釋: 0 到 0 有一個環。
解題思維:
首先,一如往常地將題目給定的邊轉換成鄰接表(Adjacency List),參見
這題。
接著我們檢查給定的圖有沒有環,而這可以使用
這題提及過的拓樸排序(Topological Sort)來檢查。只要我們找不到一個合法的拓樸排序,則代表著給定的圖不是有向無環圖(Directed Acyclic Graph,DAG)。
再接著我們把定義一個「顏色值-X」,其代表著某條路徑上顏色為 X 的節點數量。例如說,範例測資 1 中的路徑 0 → 2 → 3 → 4 的顏色值-a 為 3、顏色值-c 為 1,其餘值為 0。
可以看到此時一條路徑的顏色值為 max(顏色值-a, 顏色值-b, ……, 顏色值-z)。
因此我們定義一個二維陣列 D,其中 D[i][X] 代表著以節點 i 作為結尾的所有路徑中顏色值-X 之最大值。可以看到其遞迴式為:
如果節點 i 的 in-degree(即指向該節點的邊數)為零,則 D[i][X] = C;
(上面這條為遞迴停止條件)
如果節點 i 的 in-degree 不為零,則 D[i][X] = max(D[j][X]) + C,其中 j 為那些存在著一條邊從自身指向節點 i 的節點們。
其中如果 X == colors[i],則 C 值為 1;反之,則 C 值為 0。
而上面的遞迴式可以剛好併入前面用拓樸排序檢查有沒有環的過程之中。
也就是說每當我們要「拔掉」一個當前 in-degree 為零的節點 a 時,代表著我們已經把它的 D[a][X] 之值都求出來了(因為根據拓樸排序的定義,所有存在著路徑到節點 i 的節點全部都會先被探訪到)。
因此,我們可以把 D[a][X] 這份資訊往節點 a 指向的節點們送過去。例如說如果節點 a 有邊指向節點 b,則將 D[b][X] 之值變更為 max(D[b][X], D[a][X] + C)(注意這邊的 C 值是以 b 為準的)。一旦節點 b 的 in-degree 也變成零時,就代表著 D[b][X] 也求完了。以此類推。
最後所求則為每一個節點 N、每一種顏色 X,其對應的 D[N][X] 之值中的最大值。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。