題目連結(jié):
題目意譯:
現(xiàn)在有一條長度 n 的三線道,其由 n + 1 個(gè)編號(hào)為 0 到 n 的點(diǎn)所組成。有一隻青蛙一開始位於第二線的第 0 點(diǎn),而牠想要跳到第 n 點(diǎn)。不過,在路上可能有一些障礙物存在。
你被給定一個(gè)長度為 n + 1 的陣列 obstacles,其中 obstacles[i](其值介於 0 到 3,含端點(diǎn))代表著在第 obstacles[i] 線上的第 i 點(diǎn)上有一個(gè)障礙物。如果 obstacles[i] == 0,則代表第 i 點(diǎn)沒有障礙物。在每一個(gè)點(diǎn)上,三條線道中最多只會(huì)有一條有障礙物。
例如,如果 obstacles[2] == 1,則其代表著在第一線的第 2 點(diǎn)上有一個(gè)障礙物。
該青蛙只能在同一線道的第 i + 1 點(diǎn)上沒有障礙物時(shí)才得以從第 i 點(diǎn)跳到同一線道的第 i + 1 點(diǎn)。為了避開障礙物,該青蛙也可以側(cè)跳來跳到另一條線道的同一點(diǎn)上(即便兩線道必不相鄰),前提是目標(biāo)線道上沒有障礙物。
例如說,青蛙可以從第三線的第 3 點(diǎn)跳到第一線的第 3 點(diǎn)。
回傳該青蛙從第二線的第 0 點(diǎn)抵達(dá)任一線道的第 n 點(diǎn)上最少所需的側(cè)跳次數(shù)。
注:第 0 點(diǎn)和第 n 點(diǎn)上不會(huì)有障礙物存在。
限制:
obstacles.length == n + 1
1 ≦ n ≦ 5 × 10 ^ 5
0 ≦ obstacles[i] ≦ 3
obstacles[0] == obstacles[n] == 0
範(fàn)例測(cè)資:
範(fàn)例 1:
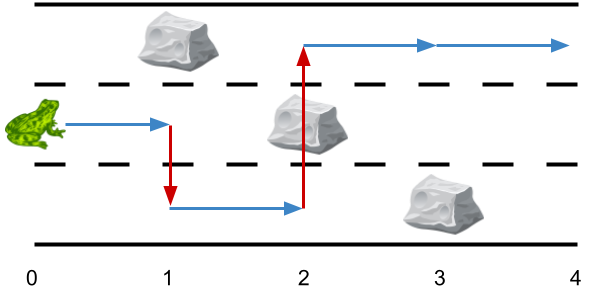
輸入: obstacles = [0,1,2,3,0]
輸出: 2
解釋: 最佳解由上圖中的箭頭所示。當(dāng)中有兩次側(cè)跳(紅色箭頭)。
注意到該青蛙只能在側(cè)跳時(shí)跳過障礙物(參見上圖中的第 2 點(diǎn))。
範(fàn)例 2:
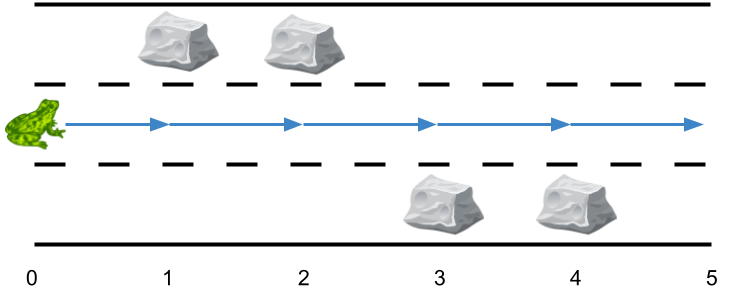
輸入: obstacles = [0,1,1,3,3,0]
輸出: 0
解釋: 第二線上沒有障礙物。不需要任何的側(cè)跳。
範(fàn)例 3:
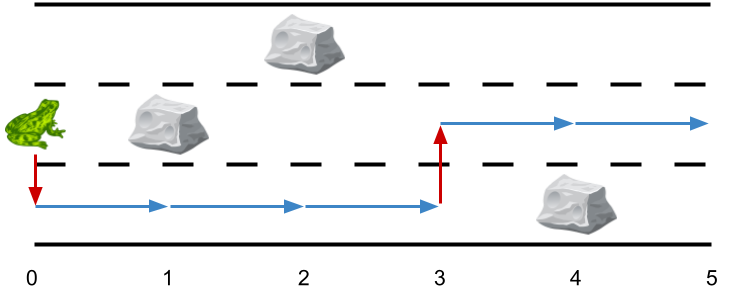
輸入: obstacles = [0,2,1,0,3,0]
輸出: 2
解釋: 最佳解由上圖中的箭頭所示。當(dāng)中有兩次側(cè)跳。
解題思維:
只要畫一個(gè)類似
這題的狀態(tài)圖(這部分交給讀者,因?yàn)榍闆r有點(diǎn)多)便可以得出這題用動(dòng)態(tài)規(guī)劃解所需的遞迴式。
定義一個(gè)二維陣列 D,其中 D[i][j] 代表著在青蛙從起點(diǎn)跳到第 j 線第 i 點(diǎn)所需的最少側(cè)跳次數(shù)。可以看到:
D[0][2] = 0(起點(diǎn))
D[0][1] = D[0][3] = 1(起點(diǎn)兩邊的線)、
如果 obstacles[i] == 1,則:
D[i][1] = 無限大(因?yàn)榍嗤艿讲涣耍?/div>
D[i][2] = min(D[i - 1][2], D[i - 1][3] + 1)(即直接從第 2 線第 i - 1 點(diǎn)跳過來,或是先從第 3 線第 i - 1 點(diǎn)跳到第 3 線第 i 點(diǎn)再跳過來)
D[i][3] = min(D[i - 1][3], D[i - 1][2] + 1)
如果 obstacles[i] == 2,則:
D[i][1] = min(D[i - 1][1], D[i - 1][3] + 1)
D[i][2] = 無限大
D[i][3] = min(D[i - 1][3], D[i - 1][1] + 1)
如果 obstacles[i] == 3,則:
D[i][1] = min(D[i - 1][1], D[i - 1][2] + 1)
D[i][2] = min(D[i - 1][2], D[i - 1][1] + 1)
D[i][3] = 無限大
如果 obstacles[i] == 0,則:
D[i][1] = min(D[i - 1][1], D[i - 1][2] + 1, D[i - 1][3] + 1)
D[i][2] = min(D[i - 1][2], D[i - 1][1] + 1, D[i - 1][3] + 1)
D[i][3] = min(D[i - 1][3], D[i - 1][1] + 1, D[i - 1][2] + 1)
可以看到答案會(huì)是 min(D[n][1], D[n][1], D[n][2])。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。