題目連結(jié):
題目意譯:
給定一個大小為 n × n 且只由 0 和 1 所組成的矩陣 grid。我們想要用一個四元樹(Quad-Tree)代表 grid。
回傳代表 grid 的四元樹之根節(jié)點。
一個四元樹為一個樹狀資料結(jié)構(gòu),其中每一個內(nèi)部節(jié)點皆有恰好四個子節(jié)點。除此之外,每個節(jié)點有兩個性質(zhì):
val:如果此節(jié)點代表著 grid 某一區(qū)域的 1,則其值為真(Ture);如果代表著某一區(qū)域的 0,則其值為假(False)。注意到你可以將那些 isLeaf 為假的節(jié)點之 val 設(shè)為真或假皆可,兩種答案都可被接受。
isLeaf:如果此節(jié)點是樹中的一個葉節(jié)點,則其值為真;反之如果該節(jié)點有四個子節(jié)點,則其值為假。
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
我們可以從一個二維區(qū)域經(jīng)由下列步驟建構(gòu)出一個四元樹:
如果當(dāng)前網(wǎng)格有著相同的數(shù)值(即全為 1 或全為 0)則將 isLeaf 設(shè)為真、 val 設(shè)為當(dāng)前網(wǎng)格的數(shù)值並將四個子節(jié)點設(shè)為空(Null)並停止分切的過程。
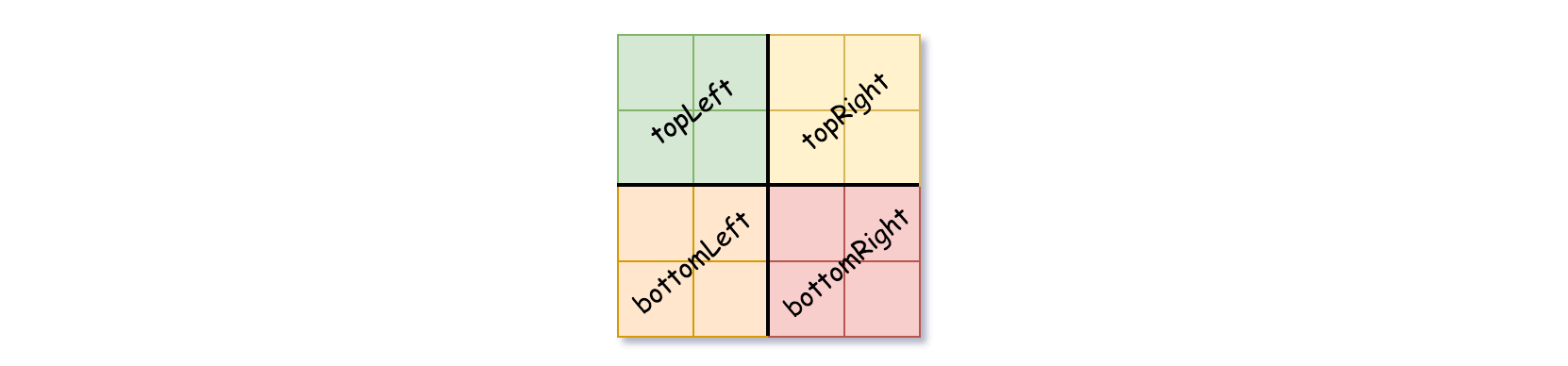
如果當(dāng)前網(wǎng)格有著不同的數(shù)值,則將 isLeaf 設(shè)為假、 val 設(shè)為任意數(shù)值並將當(dāng)前網(wǎng)格分切成四個子網(wǎng)格如下圖。
對於每個子節(jié)點以對應(yīng)的子網(wǎng)格遞迴分切下去。
(譯注:「topLeft」為「左上」、「topRight」為「右上」、「bottomLeft」為「左下」,而「bottomRight」為「右下」)
如果你想要知道更多關(guān)於四元樹的資訊,你可以參見
維基頁面。
四元樹的格式:
你不需要閱讀此部分才能解本題。這部分只是為了想瞭解輸出格式的人們。輸出代表著一個四元樹藉由階層探訪(Level-Order Traversal)的序列化(Serialized)格式,其中 null 代表著某個路徑之終點,並且這之後不存在更多節(jié)點。
這與二元樹的序列化(Serialization)非常地相似。唯一的差別是單一節(jié)點以一個列表 [isLeaf, val] 所表示。
如果 isLeaf 或 val 的數(shù)值為真,則在列表 [isLeaf, val] 中我們將以數(shù)字 1 表示;而反之若數(shù)值為假,則以數(shù)字 0 表示。
限制:
n == grid.length == grid[i].length
n == 2 ^ x where 0 ≦ x ≦ 6
範(fàn)例測資:
範(fàn)例 1:
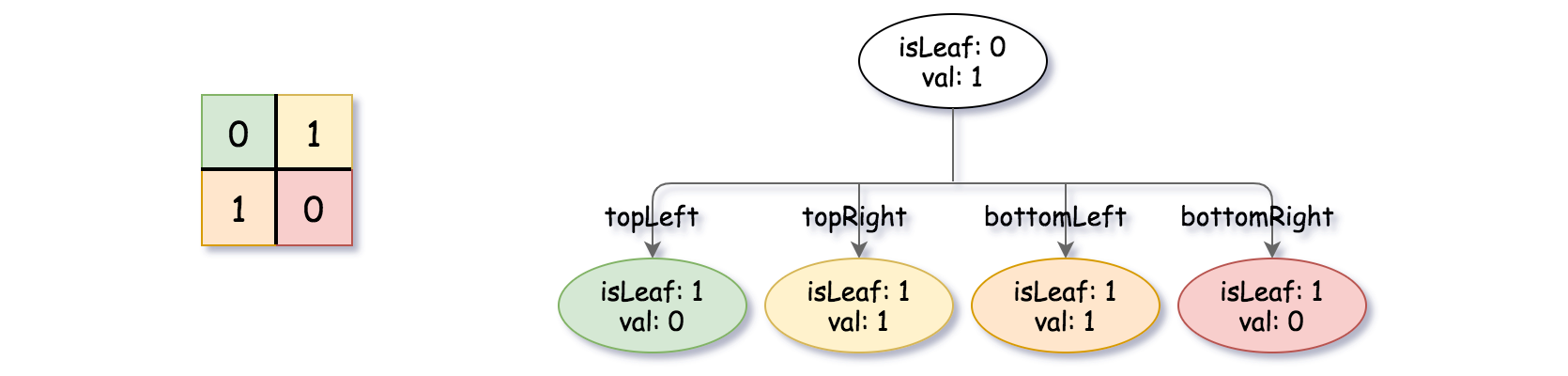
輸入: grid = [[0,1],[1,0]]
輸出: [[0,1],[1,0],[1,1],[1,1],[1,0]]
解釋: 這個例子的解釋為以下:
注意到代表四元樹的圖中 0 代表著假而 1 代表著真。
範(fàn)例 2:
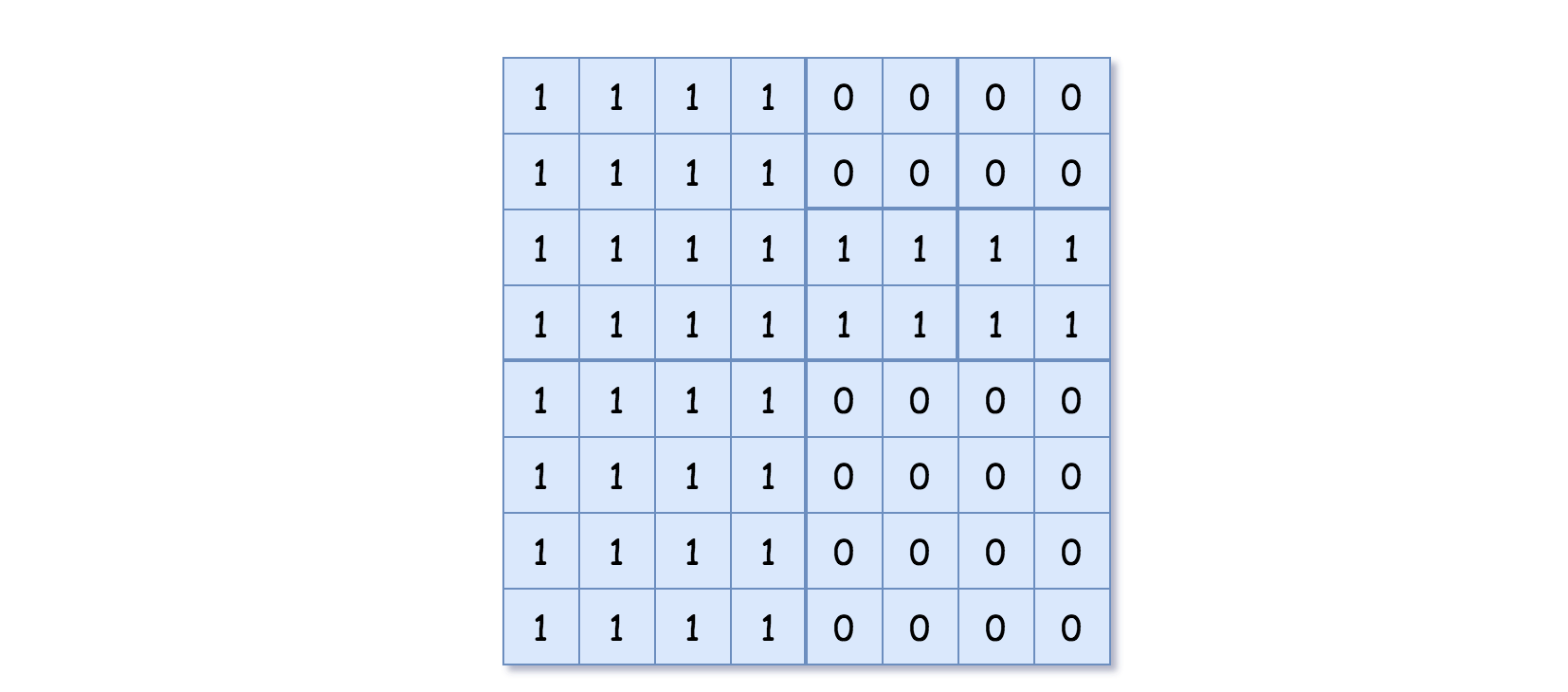
輸入: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
輸出: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
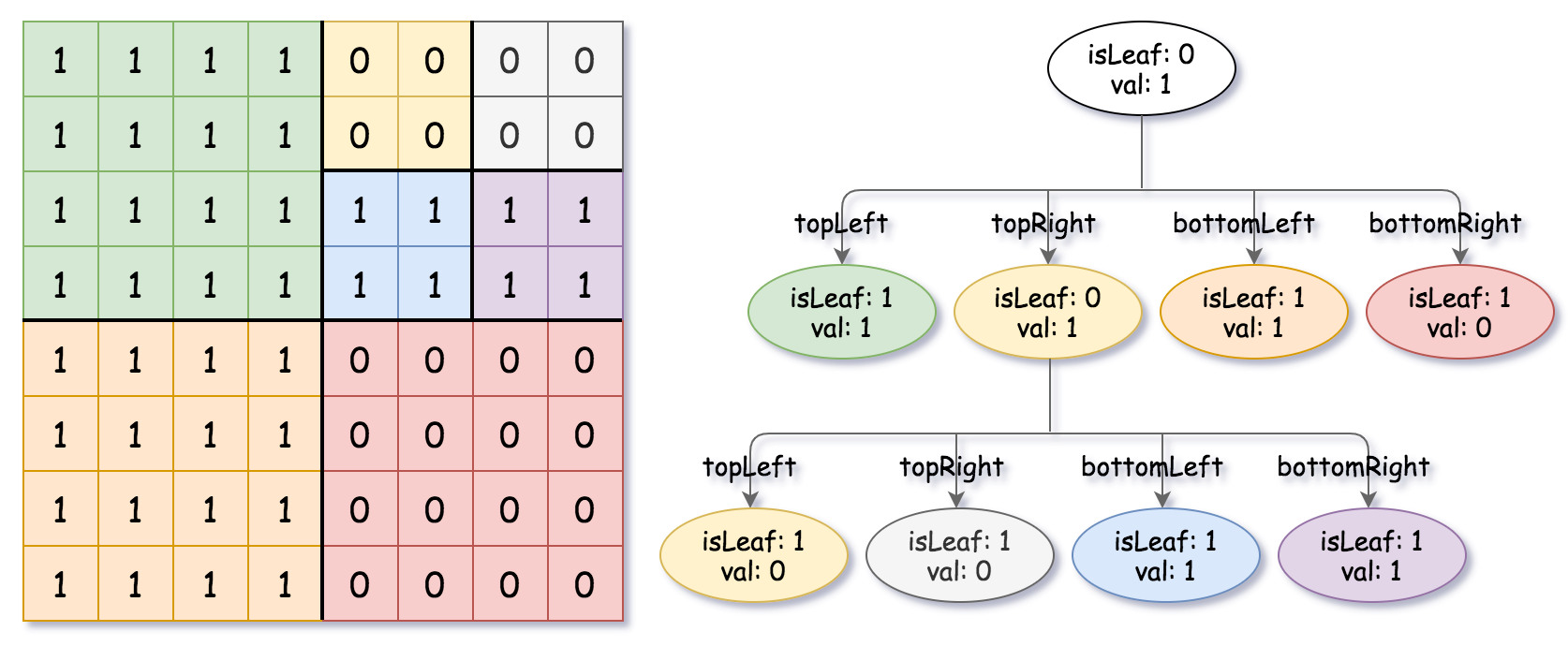
解釋: grid 中所有數(shù)字皆不相同。我們將網(wǎng)格分成四個子網(wǎng)格。
topLeft 、 bottomLeft 和 bottomRight 各自有著相同的數(shù)值。
topRight 有著不同的數(shù)字在其中,所以我們將其再分切成四個子網(wǎng)格,其中每一個各自有著相同的數(shù)值。
下圖表示了此四元樹:
解題思維:
遞迴模擬即可。
由於 grid 大小最大也只有 64 × 64,因此每一次分切時直接重新掃過一次來檢查當(dāng)前網(wǎng)格數(shù)值是否相同也是可被接受的(不需要二維前綴和(Prefix Sums)之類的來加速判斷)。
檢查完之後,如果一樣則停止分切;反之則繼續(xù)按照題目的要求來分切(由於題目的條件之緣故,因此不需要考慮沒辦法切得剛剛好)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。