題目連結(jié):
題目意譯:
你被給定一棵樹(即一個(gè)連通的、無(wú)向的圖,且其無(wú)環(huán))由編號(hào)為 0 到 n - 1 的 n 個(gè)節(jié)點(diǎn)以及恰好 n - 1 條邊所組成。樹的根節(jié)點(diǎn)為節(jié)點(diǎn) 0,而每個(gè)節(jié)點(diǎn)都會(huì)有一個(gè)標(biāo)籤,其為一個(gè)小寫字元且以一字串 labels 給定(即編號(hào) i 的節(jié)點(diǎn)之標(biāo)籤為 labels[i])。
邊的陣列 edges,其格式為 edges = [ai, bi],其代表著在樹中節(jié)點(diǎn) ai 到節(jié)點(diǎn) bi 之間有一條邊連接著。
回傳一個(gè)大小為 n 的陣列 ans,其中 ans[i] 為以節(jié)點(diǎn) i 作為根節(jié)點(diǎn)的子樹之中有多少節(jié)點(diǎn)之標(biāo)籤與節(jié)點(diǎn) i 相同。
一樹 T 之子樹為以 T 中某個(gè)節(jié)點(diǎn)以及其所有後代節(jié)點(diǎn)所組成。
限制:
1 ≦ n ≦ 10 ^ 5
edges.length == n - 1
edges[i].length == 2
0 ≦ ai, bi < n
ai != bi
labels.length == n
labels 只由小寫英文字母組成。
範(fàn)例測(cè)資:
範(fàn)例 1:
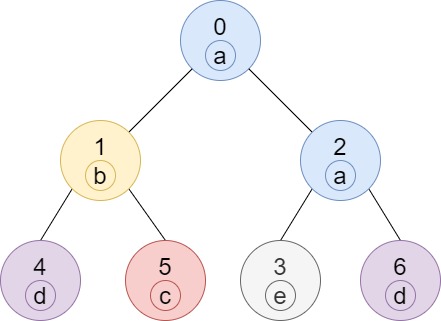
輸入: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
輸出: [2,1,1,1,1,1,1]
解釋: 節(jié)點(diǎn) 0 有著標(biāo)籤 'a' 而其子樹存在標(biāo)籤也為 'a' 節(jié)點(diǎn) 2,因此答案為 2。注意到任何節(jié)點(diǎn)都是自己的子樹之一部份。
節(jié)點(diǎn) 1 有著標(biāo)籤 'b'。節(jié)點(diǎn) 1 的子樹包含著節(jié)點(diǎn) 1 、 4 和 5,由於節(jié)點(diǎn) 4 和 5 都有著不同的標(biāo)籤,因此答案為 1(該節(jié)點(diǎn)本身)。
範(fàn)例 2:
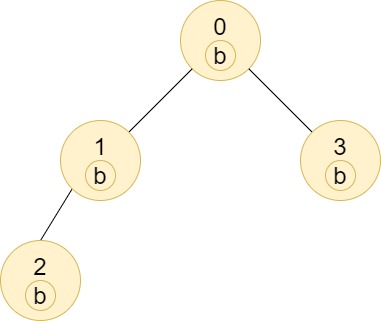
輸入: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
輸出: [4,2,1,1]
解釋: 節(jié)點(diǎn) 2 的子樹只包含節(jié)點(diǎn) 2,因此答案為 1。
節(jié)點(diǎn) 3 的子樹只包含節(jié)點(diǎn) 3,因此答案為 1。
節(jié)點(diǎn) 1 的子樹包含節(jié)點(diǎn) 1 和 2,兩者都有著標(biāo)籤 'b',因此答案為 2。
節(jié)點(diǎn) 0 的子樹包含節(jié)點(diǎn) 0 、 1 、 2 和 3,全部都有著標(biāo)籤 'b',因此答案為 4。
範(fàn)例 3:
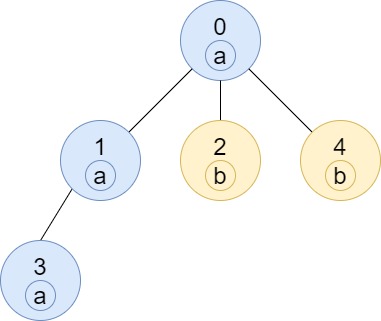
輸入: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
輸出: [3,2,1,1,1]
解題思維:
一樣遞迴求解即可,即深度優(yōu)先搜尋(Depth First Search,DFS)。
這次要記錄的是某個(gè)節(jié)點(diǎn) i 其所有子樹的每一種字母出現(xiàn)次數(shù),如果節(jié)點(diǎn) i 的標(biāo)籤是 C,則 ans[i] 即為所有子樹中 C 的出現(xiàn)次數(shù) + 1。算完 ans[i] 之後,將 C 的出現(xiàn)次數(shù) + 1 並往遞迴的上一層回傳。
最後整個(gè)遞迴跑完之時(shí),即可得到所求陣列 ans。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。