題目連結:
題目意譯:
你被給定一個索引值從 0 開始的整數陣列 nums,其長度為 2 的一個冪次。
將以下演算法套用至 nums 上:
1. 令 n 為 nums 之長度。如果 n == 1,則結束此過程;反之,創造一個新的索引值從 0 開始之陣列 newNums,且其長度為 n ÷ 2。
2. 對於每個偶數索引值 i,其中 0 ≦ i < n ÷ 2,將 newNums[i] 之值設為 min(nums[2 × i], nums[2 × i + 1])。
3. 對於每個奇數索引值 i,其中 0 ≦ i < n ÷ 2,將 newNums[i] 之值設為 max(nums[2 × i], nums[2 × i + 1])。
4. 將陣列 nums 替換成 newNums。
5. 從步驟 1 開始重複此過程。
回傳套用此演算法後 nums 最後留下來的數字。
限制:
1 ≦ nums.length ≦ 1024
1 ≦ nums[i] ≦ 10 ^ 9
nums.length 為 2 的一個冪次。
範例測資:
範例 1:
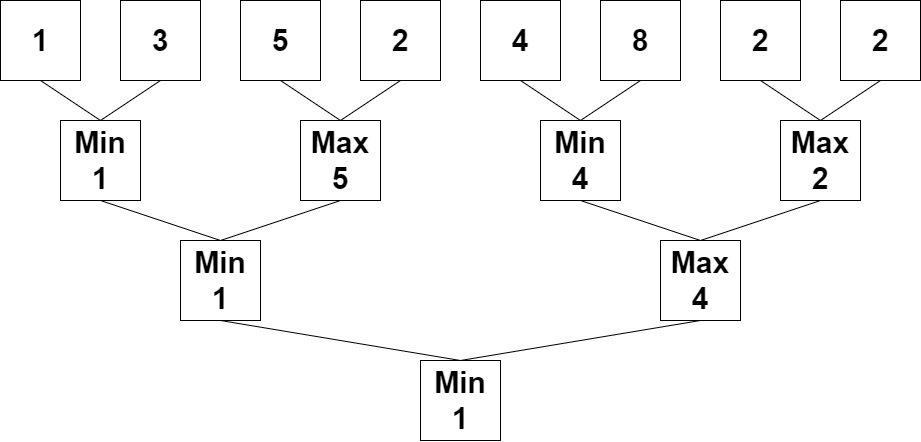
輸入: nums = [1,3,5,2,4,8,2,2]
輸出: 1
解釋: 下列陣列為重複套用該演算法的結果。
第一次: nums = [1,5,4,2]
第二次: nums = [1,4]
第三次: nums = [1]
1 為最後剩下的數字,所以我們回傳 1。
範例 2:
輸入: nums = [3]
輸出: 3
解釋: 3 已經是最後剩下的數字了,所以我們回傳 3。
解題思維:
直接模擬該演算法即可。
由於每次是直接砍掉一半的元素數量,直到最後剩下一個元素為止。因此時間複雜度為 O(n) + O(n ÷ 2) + O(n ÷ 4) + …… = O(2n) = O(n),即線性時間。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。