題目連結(jié):
題目意譯:
現(xiàn)在存在著一個(gè)有著 n 個(gè)節(jié)點(diǎn)無向樹,節(jié)點(diǎn)編號(hào)為 0 到 n - 1。
你被給定一個(gè)索引值從 0 開始且長(zhǎng)度為 n 的整數(shù)陣列 nums,其中 nums[i] 代表第 i 個(gè)節(jié)點(diǎn)的數(shù)值。你同時(shí)也被給定一個(gè)二維且長(zhǎng)度 n - 1 的整數(shù)陣列 edges,其中 edges[i] = [ai, bi] 代表著在樹中節(jié)點(diǎn) ai 和節(jié)點(diǎn) bi 之間有一條邊。
你被允許刪掉其中一些邊,將該樹分拆成若干個(gè)連通元件(Connected Components)。令一個(gè)元件的數(shù)值為 nums[i] 之總和,其中節(jié)點(diǎn) i 位於該元件之中。
回傳你最多可以刪除的邊數(shù),使得樹中每個(gè)連通元件之?dāng)?shù)值相同。
限制:
1 ≦ n ≦ 2 × 10 ^ 4
nums.length == n
1 ≦ nums[i] ≦ 50
edges.length == n - 1
edges[i].length == 2
0 ≦ edges[i][0], edges[i][1] ≦ n - 1
edges 代表著一個(gè)合法的樹。
範(fàn)例測(cè)資:
範(fàn)例 1:
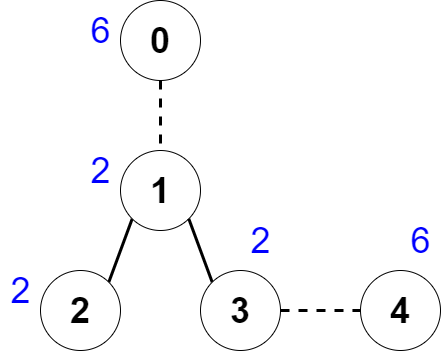
輸入: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
輸出: 2
解釋: 上圖顯示著我們可以刪除 [0,1] 和 [3,4] 這些邊。因此而得的連通元件依序?yàn)?[0] 、 [1,2,3] 和 [4]。每一個(gè)元件的數(shù)值皆等於 6。可以證明沒有更好的刪除方式存在,所以答案為 2。
範(fàn)例 2:
輸入: nums = [2], edges = []
輸出: 0
解釋: 沒有可以刪除的邊存在。
解題思維:
首先從輸入給定的 edges 建立出圖的鄰接表(Adjacency List,如
這題)。
可以看到每個(gè)元件的總和都一樣的話,則代表著該總和值為原本的樹全部節(jié)點(diǎn)值之總和(令此全節(jié)點(diǎn)值總和為 T)的一個(gè)因數(shù)。
因此我們可以掃過 T 的每一個(gè)因數(shù),而實(shí)際上我們不需要掃過 1 ~ T 的所有整數(shù),只要掃過 1 ~ sqrt(T) 即可知道 T 有哪些因數(shù)。其中 sqrt(x) 代表為 x 的平方根。
所以如果我們知道可以把原本的樹分拆成若干個(gè)各自總和為 Q 的元件,其中 Q 為 T 的一個(gè)因數(shù)。則可以看到元件總數(shù)為 T ÷ Q。而因?yàn)槲覀兊膱D是一棵「樹」,因此每刪掉一條邊便會(huì)把一個(gè)元件一分為二。因此對(duì)於 Q 來說,我們需要?jiǎng)h掉 T ÷ Q - 1 條邊形成這些元件。
那要怎麼檢查一個(gè)因數(shù) Q 可不可行呢?只要把隨便一個(gè)點(diǎn)當(dāng)作這棵無向且無根的樹之根節(jié)點(diǎn)(在這邊,以節(jié)點(diǎn) 0 作為根節(jié)點(diǎn))。則我們只要從這邊遞迴求解即可:
當(dāng)我們位於節(jié)點(diǎn) i 時(shí),我們可以先遞迴其所有子樹。而每個(gè)子樹的回傳值是各自試圖分完總和值恰好為 Q 的元件後剩下的節(jié)點(diǎn)總和值(注意:其值不一定小於 Q)。
接著把每一個(gè)子樹的剩餘的數(shù)值(回傳值)再加上節(jié)點(diǎn) i 的數(shù)值加總後,判斷一下該總和值是否恰好為 Q。如果是則將目前整體已分出來的元件數(shù),並回傳 0(因?yàn)閯偤脹]有剩餘的數(shù)值);反之,則直接回傳該總和值(即便總和值 > Q),因?yàn)檫@些節(jié)點(diǎn)目前無法形成一個(gè)元件。
最後所有節(jié)點(diǎn)的結(jié)果都求完之後,最後檢查總計(jì)形成的元件數(shù)是否恰好為 T ÷ Q 個(gè)。如果不是則代表 Q 是不可行的。
而當(dāng)中所有可行的 Q 值中,越小者越好,因?yàn)榭梢孕纬筛嗟脑6?shù)最大值減去 1 之後,即是我們所求的最多可刪除邊數(shù)。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。