題目連結:
題目意譯:
給定一棵二元樹,其節點值為 1 到 9 的數字。在二元樹中,一個路徑如果滿足路徑上的節點值至少有一個排列是迴文,則該路徑將被稱為是一個偽迴文。
回傳從根節點到葉節點的偽迴文路徑之個數。
限制:
樹中的節點個數位於範圍 [1, 10 ^ 5]。
1 ≦ Node.val ≦ 9
範例測資:
範例 1:
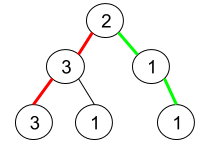
輸入: root = [2,3,1,3,1,null,1]
輸出: 2
解釋: 上圖代表著給定的二元樹。有三條路徑是從根節點走到葉節點:紅色路徑 [2,3,3]、綠色路徑 [2,1,1] 以及路徑 [2,3,1]。在這些路徑中,只有紅色路徑和綠色路徑是偽迴文,因為紅色路徑 [2,3,3] 可以重新排列成 [3,2,3](迴文),而綠色路徑 [2,1,1] 可以被重新排列成 [1,2,1](迴文)。
範例 2:
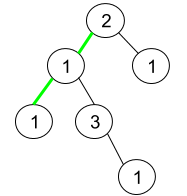
輸入: root = [2,1,1,1,3,null,null,null,null,null,1]
輸出: 1
解釋: 上圖代表著給定的二元樹。有三條路徑是從根節點走到葉節點:綠色路徑 [2,1,1]、路徑 [2,1,3,1] 和 [2,1]。在這些路徑中,只有綠色路徑是偽迴文,因為綠色路徑 [2,1,1] 可以被重新排列成 [1,2,1](迴文)。
範例 3:
輸入: root = [9]
輸出: 1
解題思維:
其實就是對根節點進行深度優先搜尋(Depth First Search,DFS),並在路上記錄過程中(即根節點到當前節點)有經過的數值各個種類之數量。
而到葉節點的時候就檢查現在這條路徑上的數字是否可以組成迴文——即判斷出現奇數次的數值有幾個(假設為 C 個),如果 C > 1 則不可能形成迴文;反之則可(出現奇數次的擺正中間,剩下的對稱地擺即可)。
最後 DFS 的過程結束後便可以知道有多少條根節點到葉節點的路徑,而其中又有多少可以形成迴文,其即為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。