題目連結(jié):
題目意譯:
你被給定一棵節(jié)點(diǎn)值皆相異的二元樹(shù)之根節(jié)點(diǎn) root,以及一整數(shù) start。在第 0 分鐘,有一例感染開(kāi)始於數(shù)值為 start 的節(jié)點(diǎn)。
每一分鐘,如果以下情況皆為真,則某節(jié)點(diǎn)將被感染:
該節(jié)點(diǎn)目前尚未被感染;
該節(jié)點(diǎn)相鄰於一個(gè)被感染的節(jié)點(diǎn)。
回傳整棵樹(shù)被感染所需的分鐘數(shù)。
限制:
樹(shù)中的節(jié)點(diǎn)數(shù)位於範(fàn)圍 [1, 10 ^ 5] 中。
1 ≦ Node.val ≦ 10 ^ 5
每個(gè)節(jié)點(diǎn)值彼此相異。
有著節(jié)點(diǎn)值 start 的節(jié)點(diǎn)必定存在於樹(shù)中。
範(fàn)例測(cè)資:
範(fàn)例 1:
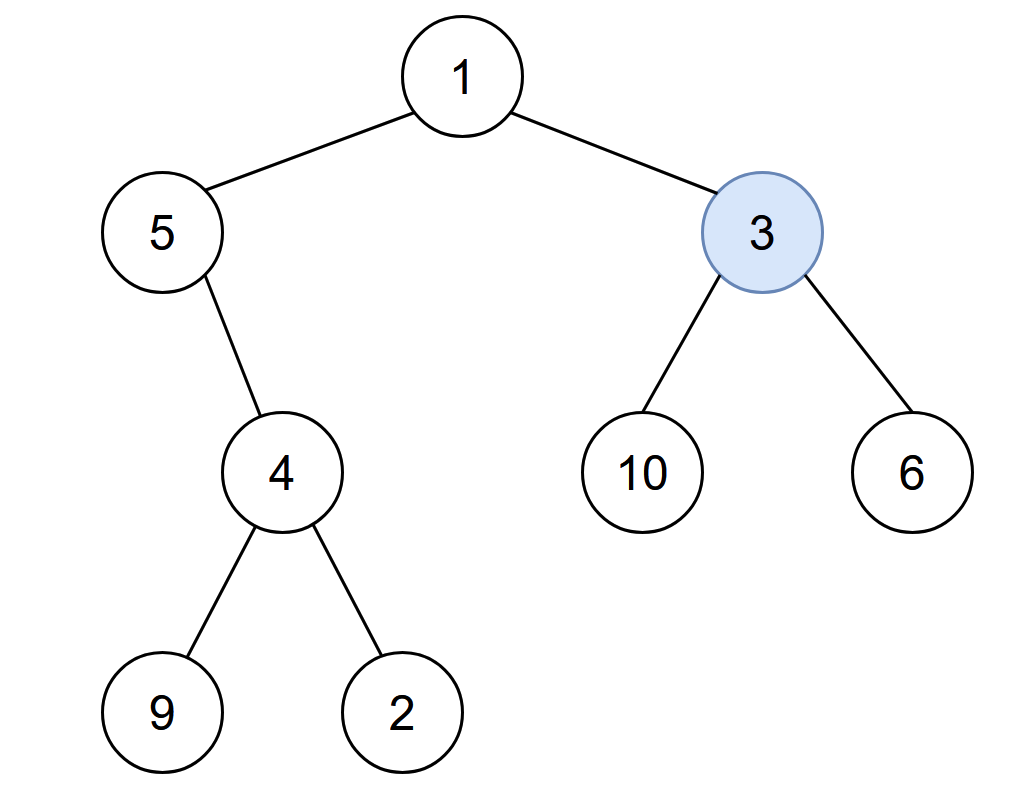
輸入: root = [1,5,3,null,4,10,6,9,2], start = 3
輸出: 4
解釋?zhuān)?以下節(jié)點(diǎn)的感染時(shí)間點(diǎn)各自為:
- 第 0 分鐘:節(jié)點(diǎn) 3
- 第 1 分鐘:節(jié)點(diǎn) 1 、 10 和 6
- 第 2 分鐘:節(jié)點(diǎn) 5
- 第 3 分鐘:節(jié)點(diǎn) 4
- 第 4 分鐘:節(jié)點(diǎn) 9 和 2
整棵樹(shù)需要 4 分鐘才會(huì)全數(shù)感染,所以我們回傳 4。
範(fàn)例 2:
輸入: root = [1], start = 1
輸出: 0
解釋?zhuān)?在第 0 分鐘,樹(shù)中唯一的節(jié)點(diǎn)被感染了,所以我們回傳 0。
解題思維:
典型的廣度優(yōu)先搜尋(Breadth First Search,BFS)題型,不過(guò)前提是你要先知道節(jié)點(diǎn)值為 start 的節(jié)點(diǎn)在哪。而它的位置可以由深度優(yōu)先搜尋(Depth First Search,DFS)或是另一次 BFS 而找到。
一旦找到,並且你在找尋該目標(biāo)節(jié)點(diǎn)(稱(chēng)其為 X)的過(guò)程順便把每個(gè)節(jié)點(diǎn)的父節(jié)點(diǎn)建立出來(lái)(為了等下方便),此時(shí)你就可以從 X 出發(fā)利用 BFS 的精神擴(kuò)散出去(如
這題等)。在擴(kuò)散的過(guò)程中統(tǒng)計(jì)「步數(shù)」(即題目中的分鐘數(shù)),最後即可知道需要多少分鐘才能感染全部節(jié)點(diǎn)。
不過(guò)實(shí)際上也可以直接進(jìn)行 DFS,而且可以塞在同一次(同一個(gè)函式)探訪(fǎng)之中。有興趣的讀者可以參見(jiàn)範(fàn)例程式碼。
大提示:每個(gè)節(jié)點(diǎn)的遞迴結(jié)果分成兩個(gè)部分。一個(gè)是「深度」,另一個(gè)則是「感染所需分鐘數(shù)」。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。