昨天說過,
標準差是一個集合中所有元素與平均數的差異程度。
提到差異會想到的是什麼?
簡單說就是「距離」。
那麼數學上,
「距離」該怎麼求呢?
以一維空間來說,
很簡單,
兩個數字相減取絕對值就好了。
例如 3 跟 5 的距離,
就是 5-3=2。
那我們拓展一下,
如果是二維空間上的兩點怎麼取距離?
這時就要祭出畢氏定理。
兩點的 X 座標相減取絕對值算出 X 方向的距離,
接著 Y 座標也依樣炮製,
接著把兩個數字取平方和再開根號。
例如 (1,2) 跟 (4,6) 的距離,
X 方向距離為 3,
Y 方向距離為 4,
所以兩點的距離就是 √(9+16)=5。
那我們再拓展一下,
如果是三維空間上的兩點怎麼取距離?
一樣利用畢氏定理,
先求兩點在 XY 平面上投影的距離與 Z 方向距離,
接著把兩數都平方相加後開根號。
而 XY 平面上投影的平方實際上就是 X 方向距離與 Y 方向距離的平方和對吧?
所以就得到結論,
各方項的距離平方和再開根號就是兩點距離了。
換句話說,
對於 n 維空間上的兩點取距離,
其公式就是兩點在各個維度上的距離平方和再開根號。
那麼回到統計學的標準差上。
標準差既然指的是整個資料與平均值的「距離」,
那是不是也能以同樣的方式計算呢?
當然可以。
事實上,
這就是標準差的定義。
假設我們有一個集合,
裡面有 n 個元素,
而這些元素一定有一個平均數 a。
舉例來說,
假設一個集合 S 包含 5 個元素,
分別是 6 7 8 9 10,
那麼平均數就是 8。
如果我們想把整個集合裡的元素以一個點表示,
那麼這個點就包含 n 個維度的變數,
換句話說,
整個集合相當於一個 n 維空間裡的一個點。
以上數的集合 S 來舉例,
它就是一個五維空間中的點,
座標是 (6,7,8,9,10)。
集合 S 的平均數是 8,
我們想像有一個集合叫做 A,
A 的維度要跟 S 一樣且所有變數都是 S 的平均數,
那麼我們就可以說集合 A 是集合 S 的平均數。
那麼求 A 跟 S 的距離,
就是集合 S 中每一個元素與平均數的距離了。
以集合 S 來說,
就是求 (6,7,8,9,10) 與 (8,8,8,8,8) 的距離,
答案是 √(4+1+0+1+4)=√10
但是這裡有一個重點,
這裡指的是「所有元素」與平均數的距離,
所以很顯然的元素越多這個數值會越大嘛!
那我們要求每個元素與平均數的平均距離怎麼求?
那就除以元素數就好了。
這個就是標準差的定義。
換句話說,
我們可以把公式寫成這樣:

當中,
σ 代表標準差,
n 代表元素數,
i 代表元素編號(第 1 個到第 n 個),
a 代表平均數。
這個式子我們可以進一步化簡:
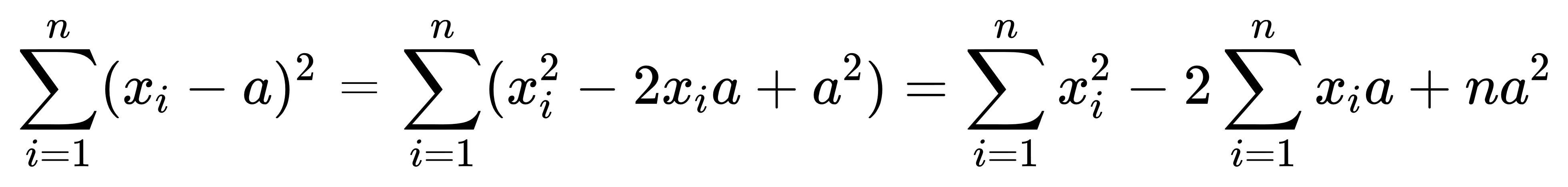
後面求和的部分獨立提出來,
括號裡面直接展開成三項,
然後對三項個別求和再相加,
其值不變。
當中第三項的a平方因為要連續加n次,
所以就是na平方。
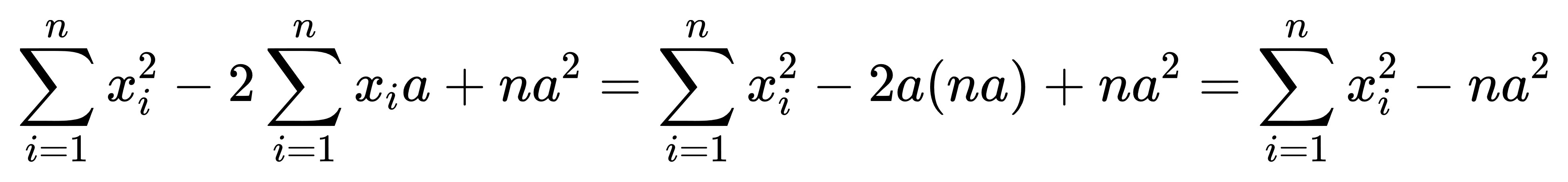
進一步化簡,
因為平均值是常數,
所以可以提到求和記號之外。
然後平均數是什麼意思?
平均數的意思不就是每一個元素相加總後除以元素數嗎?
所以 n 個元素加總的合計值,
就是平均數的 n 倍可以理解吧?
因此第二項解出來就是 2a(na),
也就是2na平方。
最後,
既然第二項跟第三項都有 na平方,
那我們就能把兩項合併起來。
第二項的係數是 -2 而第三項的係數是 1,
因此合併後就變成-na平方。
所以帶回去標準差的公式裡:
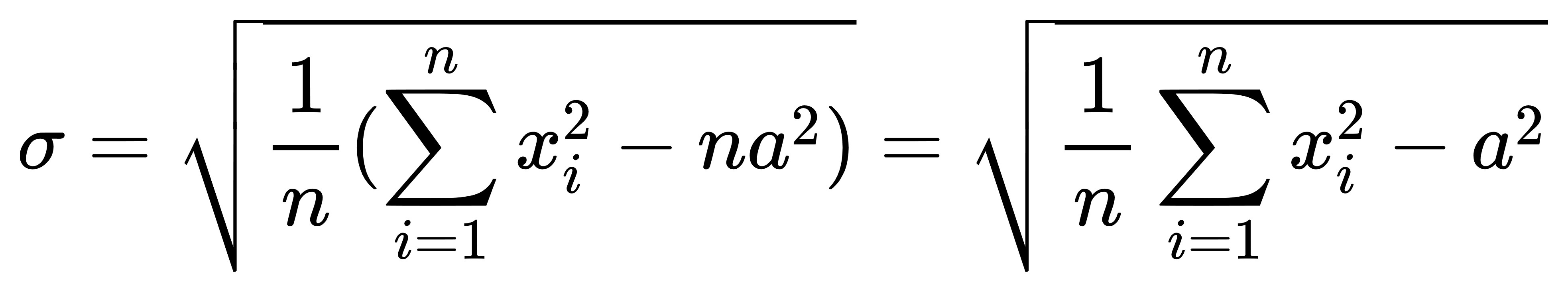
因為要乘上 n 分之 1,
所以na平方的n就消掉了,
因此把括號展開後就變成後面的樣子。
於是跟號底下就變成,
「每一個元素的平方求和後除以n」,
再減去平均數的平方。
除以n不就是求平均?
只是這個平均是每個元素平方後的平均,
因此有了口訣:平方的平均減去平均的平方。
這裡我們補充一個概念:變異數。
變異數顧名思義,
就是「變異的程度」。
其定義就是每個元素與平均數的差距的平方的平均數。
用中文表達起來很複雜,
其實變異數的定義就是:

欸嘿,
就這麼巧,
變異數剛好是標準差的平方欸。
變異數在統計學上的意義,
概念上跟標準差有點類似。
變異數是「元素的離散程度」,
標準差是「元素與平均數的平均距離」,
雖然定義不同,
但總歸來說都是在講你這組數據每個元素間的差異量有多大的指標。
然而,
一般應用上人們對變異數 Var 並不關心,
因為變異數的單位與元素的單位不一樣。
關於單位問題,
敝人在兩年前的這篇文章中有特別提到,
在運算過程中(不論是相乘、相除、平方還是開方),
「單位」本身也必須被納入計算而不能獨立於數字之外。
既然變異數的公式是元素與平均數的差異的「平方和」的平均,
當然它的單位就是平方單位,
因此變異數的單位與我們關心的數據不同,
這導致我們很難做後續的計算。
而標準差因為開了一次平方根,
因此單位就又變成跟原始數據相同了。
既然單位相同那就可以相加減啦!
因此在使用上人們更傾向於使用「標準差」。
然而,
在計算標準差的過程中必然得先求出變異數,
因此雖然變異數不常使用,
卻總是形影不離。
做個實際例子吧,
假設有 3 個人,
身高分別是 150 公分、155 公分、175 公分,
那麼平均數是多少?
(150+155+175)÷3=160,
因此平均數是 160 公分。
那麼變異數是多少?
既然知道平均數是 160 公分,
那麼就是 [ (150-160)^2+(155-160)^2+(175-160)^2]÷3,
也就是 ( 100 平方公分 + 25 平方公分 + 225 平方公分 )÷3 = 116.67 平方公分。
千萬要注意這裡的單位是「平方公分」而不是「公分」。
接著把 116.67 平方公分開根號,
就會得到 10.8 公分,
因此標準差就是 10.8 公分。
方才為什麼要強調單位是「平方公分」呢?
有這麼重要嗎?
當然有。
不信的話,
同樣的樣本,
我們換個單位,
換成 1.5 公尺、1.55 公尺、1.75 公尺,
一模一樣的題目喔,
平均是 1.6 公尺沒有問題,
所以變異數是多少?
套公式,
[ (1.5-1.6)^2+(1.55-1.6)^2+(1.75-1.6)^2]÷3
=(0.01+0.0005+0.0225)÷3=0.011667。
單位是什麼?
平方公尺。
來,
1平方公尺是多少平方公分?
10000平方公分。
所以116平方公分是多少平方公尺?
0.0116平方公尺。
如果單位不重要,
所以前面算出來的116如果代表116公分,
那麼這一題算出來的是不是應該要是1.16公尺嗎?
那為什麼答案會是0.0116而不是1.16?
因此單位重不重要?
超級重要。
OK,
算出變異數是 0.011667 平方公尺以後,
一樣開根號求標準差,
求得標準差是 0.108 公尺,
跟前面算的 10.8 公分結論相同。
從這個例題當中,
敝人用兩個不同的單位來描述同樣一件事情,
既然是同樣一件事情,
他們應該要有相同的答案,
以此說明單位的重要性。
因為變異數的單位太過獨特,
導致計算上不好用,
所以變異數是一個存在感很強卻沒什麼用途的數字。
人們更關心的還是它開根號後的那個標準差,
因為單位必須相同才能做加減運算。

封面圖片:AI生成
本篇使用的方程式編輯素材來自:LaTeX公式編輯器

