題目連結:
題目意譯:
你被給定一個 n × n 整數矩陣 grid。
請生成一個整數矩陣 maxLocal 其大小為 (n - 2) × (n - 2),並使得:
maxLocal[i][j] 等於以 grid[i + 1][j + 1] 為中心的 3 × 3 子矩陣中的最大值。
換句話說,我們想要找到 grid 中每個連續 3 × 3 子矩陣的最大值。
回傳生成出的矩陣。
限制:
n == grid.length == grid[i].length
3 ≦ n ≦ 100
1 ≦ grid[i][j] ≦ 100
範例測資:
範例 1:
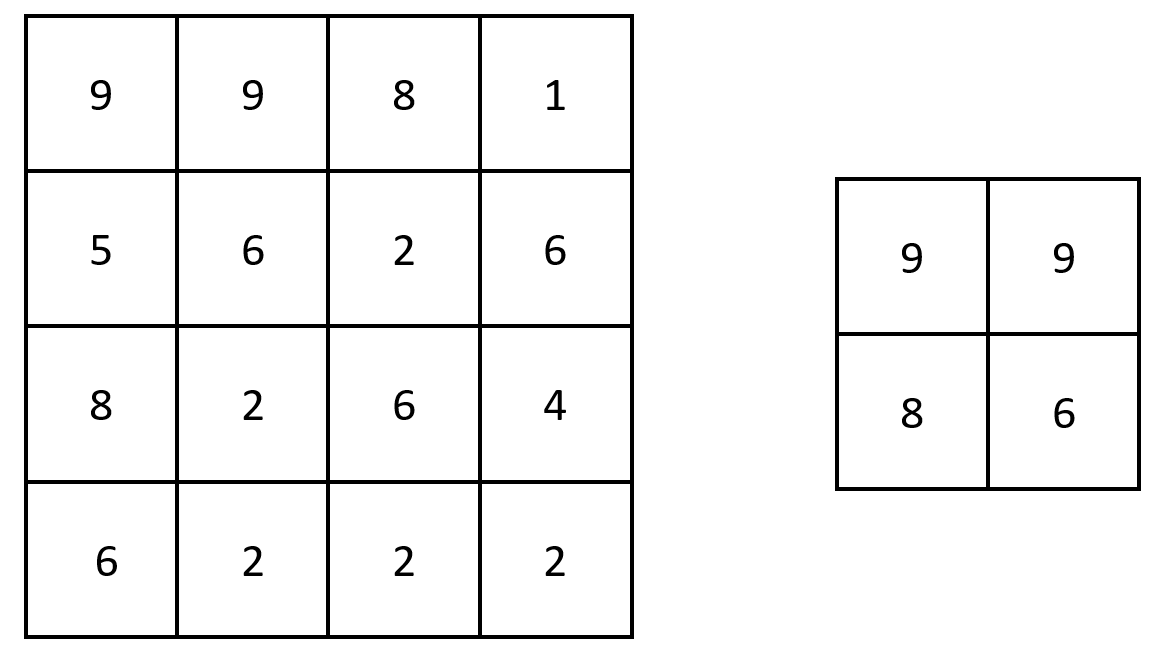
輸入: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
輸出: [[9,9],[8,6]]
解釋: 上圖顯示了原始的矩陣和生成的矩陣。
注意到生成的矩陣每個數值對應到 grid 中一個連續 3 × 3 子矩陣的最大值
範例 2:
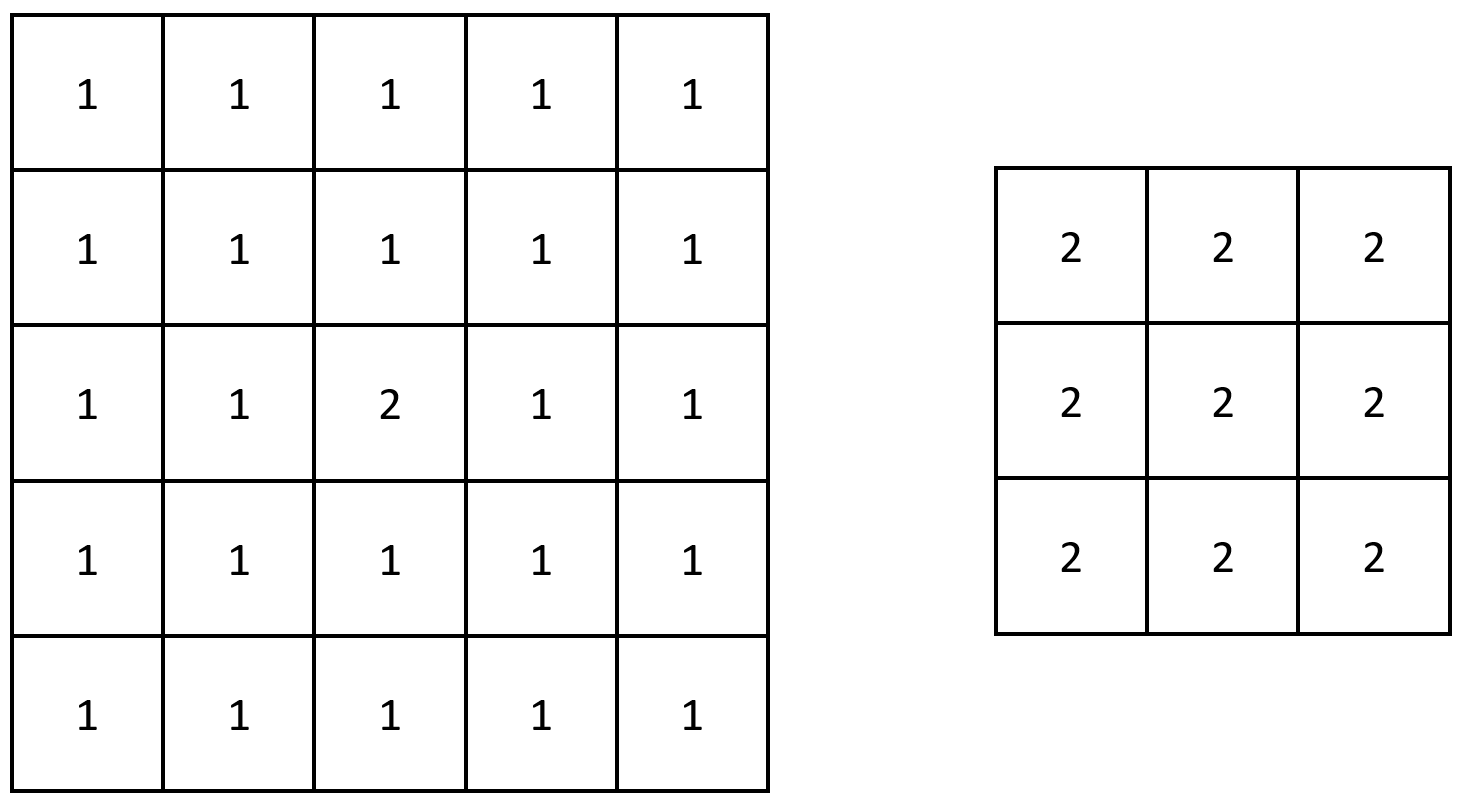
輸入: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
輸出: [[2,2,2],[2,2,2],[2,2,2]]
解釋: 注意到 2 被 grid 中每個連續 3 × 3 子矩陣所包含在內。
解題思維:
就是單純地先生成一個大小為 x × y 的矩陣 M,其中 x = n - 2 、 y = m - 2。
然後掃過 M 的每一個位置 M[i][j],找出
grid[i][j] 、 grid[i][j + 1] 、 grid[i][j + 2] 、
grid[i + 1][j] 、 grid[i + 1][j + 1] 、 grid[i + 1][j + 2] 、
grid[i + 2][j] 、 grid[i + 2][j + 1] 、 grid[i + 2][j + 2]
這九格的最大值即是 M[i][j] 之值。
掃完 M 之後便可以得到所求的矩陣。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。