題目連結(jié):
題目意譯:
你被給定一整數(shù) n。現(xiàn)在有一個(gè)包含 n 個(gè)節(jié)點(diǎn)的無向圖,這些節(jié)點(diǎn)編號(hào)為 0 到 n - 1。你被給定一個(gè)二維整數(shù)陣列 edges,其中 edges[i] = [ai, bi] 代表著存在一條無向邊連接著節(jié)點(diǎn) ai 和節(jié)點(diǎn) bi。
回傳相異節(jié)點(diǎn)的配對(duì)之?dāng)?shù)量,其中每對(duì)節(jié)點(diǎn)彼此之間無法互相連通。
限制:
1 ≦ n ≦ 10 ^ 5
0 ≦ edges.length ≦ 2 × 10 ^ 5
edges[i].length == 2
0 ≦ ai, bi < n
ai != bi
不存在重複的邊。
範(fàn)例測(cè)資:
範(fàn)例 1:
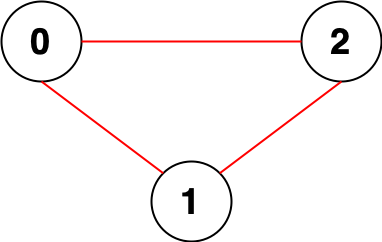
輸入: n = 3, edges = [[0,1],[0,2],[1,2]]
輸出: 0
解釋: 沒有節(jié)點(diǎn)對(duì)彼此之間無法互相連通。因此,我們回傳 0。
範(fàn)例 2:
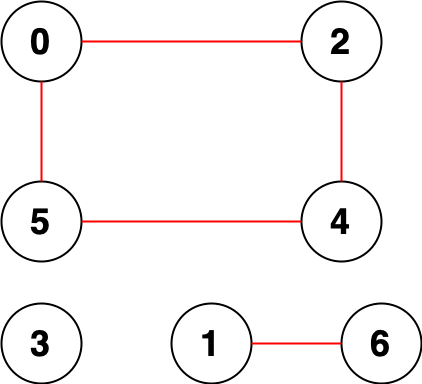
輸入: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
輸出: 14
解釋: 現(xiàn)在有 14 對(duì)節(jié)點(diǎn)對(duì)彼此之間無法互相連通:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]。
因此,我們回傳 14。
解題思維:
用跟
這題類似的方式來找出每一個(gè) component 的大小(DFS 和 BFS 的過程中統(tǒng)計(jì),而併查集則是「rank」本身就可以存大小的資訊)。
而所求的「反命題」即為求有多少節(jié)點(diǎn)可以互相連通,因此我們可以先計(jì)算出反命題的答案——根據(jù)上面求出的各個(gè) component 大小,每個(gè) component 內(nèi)部的節(jié)點(diǎn)可以彼此互通。因此一個(gè) component 將為答案貢獻(xiàn) L × (L - 1) ÷ 2,其中 L 為 component 的大小。
最後將「所有節(jié)點(diǎn)可能的配對(duì)總數(shù)」(即 n × (n - 1) ÷ 2)減去「反命題之答案」即是所求。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。