題目連結:
題目意譯:
現在有一個包含 n 個點的雙向圖,其中每一個節點編號為 0(含)到 n - 1(含)�。圖中的邊以一個二維整數陣列 edges 表示�,其中每個 edges[i] = [ui, vi] 代表著節點 ui 和節點 vi 之間有一條雙向的邊。每一個節點對最多只會被一條邊連接著�,而沒有節點會有自己到自己的邊存在��。
你想要判斷在節點 source 和節點 destination 之間有一條合法的路徑存在�。
給定 edges 和整數 n �����、 source 和 destination�����,如果存在一個合法的路徑介於 source 和 destination 之間則回傳真(True);反之��,則回傳假(False)��。
限制:
1 ≦ n ≦ 2 × 10 ^ 5
0 ≦ edges.length ≦ 2 × 10 ^ 5
edges[i].length == 2
0 ≦ ui, vi ≦ n - 1
ui != vi
0 ≦ source, destination ≦ n - 1
沒有重複的邊���。
沒有自環�����。
範例測資:
範例 1:
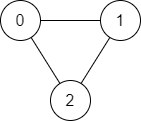
輸入: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
輸出: true
解釋: 從節點 0 到節點 2 存在兩條路徑:
- 0 → 1 → 2
- 0 → 2
範例 2:
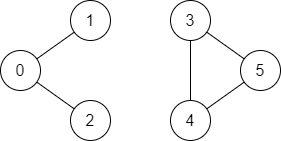
輸入: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
輸出: false
解釋: 節點 0 到節點 5 不存在任何路徑�����。
解題思維:
作法很多:
一���,可以直接從 source 進行廣度優先搜尋(Breadth First Search�,BFS)或深度優先搜尋(Depth First Search,DFS)(當然,都需要記錄哪些節點已經看過了)看是否可以抵達 destination。
二���,可以利用併查集(Union-Find Set)來檢查 source 和 destination 這兩個節點是否在同一個集合(同一個 component 即是同一個集合)中。而因為邊是雙向的�����,所以在同一個集合中代表彼此可以互通���。
此次分享到此為止����,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。