題目連結:
題目意譯:
你被給定一個索引值從 0 開始的 m × n 整數矩陣 grid,其由從 0 到 m × n - 1 的相異整數組成。你可以在該矩陣中的某一格子移動到下一列的任意格子。也就是說,如果你現在位於格子 (x, y) 滿足 x < m - 1,則你可以移動到格子 (x + 1, 0) 、 (x + 1, 1) 、 …… 、 (x + 1, n - 1) 中的任何一者。注意到在最後一列是沒辦法從任何一個格子移動的。
每個可能的移動都有著一個成本,其給定於一個索引值從 0 開始且大小為 (m × n) x n 的二維陣列 moveCost,其中 moveCost[i][j] 為從位於行 j 且帶有數值 i 的格子移動到下一列的成本。從最後一列的格子移動之成本可以忽略。
grid 中一條路徑的成本為路徑上所有格子之數值總和加上所有移動的成本。回傳在從第一列任意格子出發並抵達最後一列任一格子的最小成本。
限制:
m == grid.length
n == grid[i].length
2 ≦ m, n ≦ 50
grid 由從 0 到 m × n - 1 的相異整數組成。
moveCost.length == m × n
moveCost[i].length == n
1 ≦ moveCost[i][j] ≦ 100
範例測資:
範例 1:
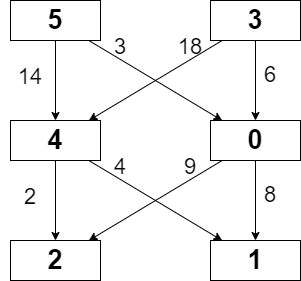
輸入: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
輸出: 17
解釋: 有著最小可能的成本為路徑 5 -> 0 -> 1。
- 路上的格子之數值總和為 5 + 0 + 1 = 6。
- 從 5 移動到 0 的成本為 3。
- 從 0 移動到 1 的成本為 8。
所以該路徑的總成本為 6 + 3 + 8 = 17。
範例 2:
輸入: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
輸出: 6
解釋: 有著最小可能的成本為路徑 2 -> 3。
- 路上的格子之數值總和為 2 + 3 = 5。
- 從 2 移動到 3 的成本為 1。
所以此路徑的總成本為 5 + 1 = 6。
解題思維:
基本上跟
這題一致,差別只有本題不會有分數的損失而且該題是「最大化分數」而本題是「最小化成本」(但作法本質一樣)而已。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。