題目連結:
題目意譯:
給定一個二元樹的根節點 root,回傳滿足條件的節點個數,其中每個節點應滿足其值等於其子樹之數值平均。
注:
n 個元素的平均為 n 個元素的總和除以 n 並將其值向下取整到最近的整數。
一節點 root 的子樹為一棵由 root 以及其所有後代節點所組成的樹。
限制:
樹中的節點數位於範圍 [1, 1000]。
0 ≦ Node.val ≦ 1000
範例測資:
範例 1:
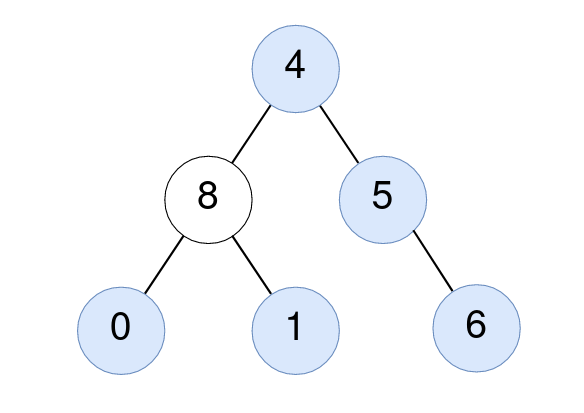
輸入: root = [4,8,5,0,1,null,6]
輸出: 5
解釋:
對於數值 4 的節點:其子樹的平均為 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4。
對於數值 5 的節點:其子樹的平均為 (5 + 6) / 2 = 11 / 2 = 5。
對於數值 0 的節點:其子樹的平均為 0 / 1 = 0。
對於數值 1 的節點:其子樹的平均為 1 / 1 = 1。
對於數值 6 的節點:其子樹的平均為 6 / 1 = 6。
範例 2:
輸入: root = [1]
輸出: 1
解釋: 對於數值 1 的節點:其子樹的平均為 1 / 1 = 1。
解題思維:
從 root 開始進行深度優先搜尋(Depth First Search,DFS)來遞迴求解即可——假設現在節點 X,且已知其左右子樹各自的節點數量 Lc 、 Rc 以及總和 Ls 、 Rs(如果 X 沒有左子節點,則視為其左子樹有 0 個節點且總和為 0。右子節點為空則同理)。
因此以節點 X 作為根節點的子樹之節點總數為 Xc = Lc + Rc + 1 且總和為 Xs = Ls + Rc + X.val。因此子樹的平均為 A = Xs / Xc。而如果此時 A 恰好等於 X.val,則所求節點個數要加上 1。
最後把 Xc 、 Xs 作為回傳值傳回到上一層遞迴。
整個遞迴過程結束後則統計過程中符合條件的節點個數即為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。