題目連結:
題目意譯:
一個二維陣列中一個尖峰元素為一元素其嚴格大於其鄰近元素,也就是其上下左右相鄰的鄰居。
給定一個索引值從 0 開始的矩陣 mat,其中沒有兩個相鄰格子是一樣的,請找到任一一個尖峰元素 mat[i][j] 並以長度 2 的陣列 [i,j] 之形式回傳。
你可以假設整個矩陣是被一整圈 -1 之值包在外側。
你必須撰寫一個演算法其時間複雜度為 O(m log(n)) 或是 O(n log(m))。
限制:
m == mat.length
n == mat[i].length
1 ≦ m, n ≦ 500
1 ≦ mat[i][j] ≦ 10 ^ 5
沒有兩個相鄰格子是一樣的。
範例測資:
範例 1:
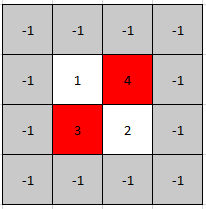
輸入: mat = [[1,4],[3,2]]
輸出: [0,1]
解釋: 3 和 4 都是尖峰元素,所以 [1,0] 和 [0,1] 都是可被接受的答案。
範例 2:
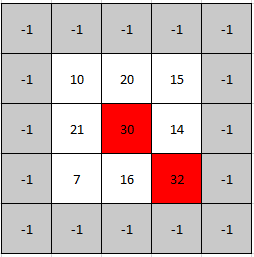
輸入: mat = [[10,20,15],[21,30,14],[7,16,32]]
輸出: [1,1]
解釋: 30 和 32 都是尖峰元素,所以 [1,1] 和 [2,2] 都是可被接受的答案。
解題思維:
其實就是
系列第一題的推廣而已。而因為現在有「第二個」方向要考慮(假設我們是對「行」做二分搜),因此我們需要先掃過一次另一個方向(承前,這邊則為「列」),看哪個元素是該方向中最大者。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。