題目連結:
題目意譯:
你被給定一正整數 n 代表著一個有向無環圖(Directed Acyclic Graph,DAG)之節點數。節點編號為 0(含)到 n - 1(含)。
你同時也被給定一個二維整數陣列 edges,其中 edges[i] = [fromi, toi] 代表著在圖中存在一條單向的邊是從 fromi 到 toi。
回傳一列表 answer,其中 answer[i] 為第 i 個節點的祖先節點之列表,其按編號大小升序排序。
如果一個節點 u 可以藉由一些邊抵達另一個節點 v,則 u 為 v 的祖先節點。
限制:
1 ≦ n ≦ 1000
0 ≦ edges.length ≦ min(2000, n × (n - 1) / 2)
edges[i].length == 2
0 ≦ fromi, toi ≦ n - 1
fromi != toi
圖中無重邊。
給定的圖為有向且無環的。
範例測資:
範例 1:
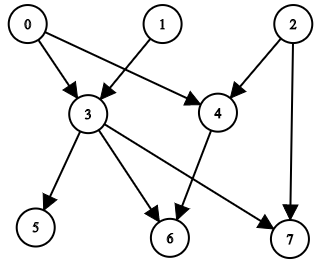
輸入: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
輸出: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解釋:
上圖代表著輸入給定的圖。
- 節點 0 、 1 和 2 沒有任何祖先節點。
- 節點 3 有兩個祖先 0 和 1。
- 節點 4 有兩個祖先 0 和 2。
- 節點 5 有三個祖先 0 、 1 和 3。
- 節點 6 有五個祖先 0 、 1 、 2 、 3 和 4。
- 節點 7 有四個祖先 0 、 1 、 2 和 3。
範例 2:
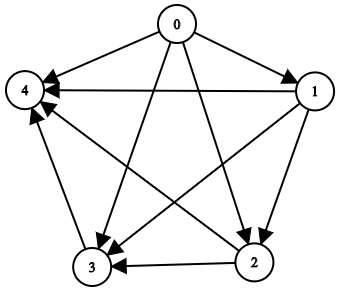
輸入: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
輸出: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
解釋:
上圖代表著輸入給定的圖。
- 節點 0 沒有任何祖先節點。
- 節點 1 有一個祖先 0。
- 節點 2 有兩個祖先 0 和 1。
- 節點 3 有四個祖先 0 、 1 、 2 和 3。
解題思維:
首先從輸入給定的 edges 建立出圖的鄰接表(Adjacency List,如
這題)。
然後窮舉每一個節點作為「祖先」,然後利用剛剛建立的鄰接表並以廣度優先搜尋(Breadth First Search,BFS)的精神來看我們可以從這個「祖先」走到哪些節點。對於每個被走到的節點 i,就將 answers[i] 加上現在這個「祖先」。
最後窮舉完便可以知道所有人的祖先。時間複雜度是 O(n × edges.length)。在本題中因為限制條件所以會被 O(n ^ 2) 限制住,但無限制的話理論上會到 O(n ^ 3)。
注:在 Leetcode 討論區會看到有些人用拓樸排序(Topological Sort,如
這題)來找到一個順序遍歷這張圖。因為這樣子下,任何當前 in-degree 是 0 的節點則代表該節點的祖先已經被找完了,所以可以從它出發到其他節點並將它以及它的祖先放到那些可抵達的節點之 answers 列表中(但是別忘了編號要由小到大)。
不過我不覺得這樣子會比較快(不管是在本題還是理論上)。我直覺認為時間複雜度將會最差是 O(V + EV log V),但是目前無法證明這個上界是緊密的(即無法再降低)。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。