題目連結(jié):
題目意譯:
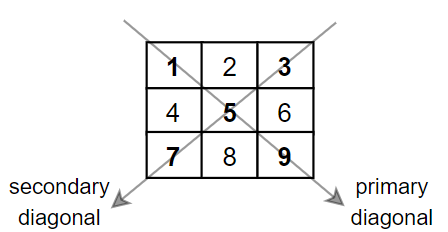
給定一個(gè)方形矩陣 mat,回傳矩陣對(duì)角線之?dāng)?shù)值總和。
總和之值只包含主對(duì)角線上所有元素以及不屬於主對(duì)角線的次對(duì)角線上之元素。
限制:
n == mat.length == mat[i].length
1 ≦ n ≦ 100
1 ≦ mat[i][j] ≦ 100
範(fàn)例測(cè)資:
範(fàn)例 1:
輸入: mat = [[1,2,3],
[4,5,6],
[7,8,9]]
輸出: 25
解釋: 對(duì)角線元素和:1 + 5 + 9 + 3 + 7 = 25
注意到 mat[1][1] = 5 只有被算到一次。
範(fàn)例 2:
輸入: mat = [[1,1,1,1],
[1,1,1,1],
[1,1,1,1],
[1,1,1,1]]
輸出: 8
範(fàn)例 3:
輸入: mat = [[5]]
輸出: 5
解題思維:
可以看到如果方陣 mat 的寬度為奇數(shù),則主對(duì)角線和次對(duì)角線會(huì)重疊於 mat[(n - 1) ÷ 2][(n - 1) ÷ 2] 這個(gè)元素;偶數(shù)則不會(huì)重疊。
因此我們可以直接先把主對(duì)角線,即 mat[0][0] 、 mat[1][1] 、……,和次對(duì)角線,即 mat[0][n - 1] 、 mat[1][n - 2] 、……,上的元素全數(shù)加總。然後看 n 是否為奇數(shù),來(lái)判斷有無(wú)重疊的元素。有就減去重複(如上提及)再回傳;反之就直接回傳即可。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。