題目連結:
題目意譯:
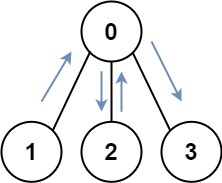
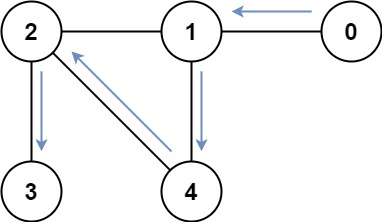
你有一個無向連通圖,其節點數為 n 個且編號為 0 到 n - 1。你被給定一個陣列 graph,其中 graph[i] 為節點 i 藉由某條邊連接到的所有節點所形成的列表。
回傳探訪所有節點的最短路徑之長度。你可以開始或結束於任意節點,你也可以重複造訪同一個節點數次,而且你可以重複使用同一條邊。
限制:
n == graph.length
1 ≦ n ≦ 12
0 ≦ graph[i].length < n
graph[i] 不包含 i。
如果 graph[a] 包含 b,則 graph[b] 包含 a。
輸入的圖保證連通。
範例測資:
範例 1:
輸入: graph = [[1,2,3],[0],[0],[0]]
輸出: 4
解釋: 其中一個可能的路徑為 [1,0,2,0,3]
範例 2:
輸入: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
輸出: 4
解釋: 其中一個可能的路徑為 [0,1,4,2,3]
解題思維:
可以看到節點數最多才 12 個。因此如果使用一個二進位數字來表示每一個節點「目前」有沒有被探訪過,該數字最多也只需要 12 個位元,即 2 ^ 12 種狀態。
所以我們可以仿造以前解旅行推銷員問題(Travelling Salesman Problem,TSP)時的作法,如
這題——即定義一個二維陣列 D[i][j],其中 i 代表著目前每個節點被探訪之狀態(即上面提及之最長 12 位元之二進位數字)、j 代表著目前位於哪個節點,而整個 D[i][j] 代表著在 i 這個狀態且位於節點 j 的情況下,探訪完剩下的節點之最短路徑。
而我們可以看到其遞迴式即為
D[i][j] = min(D[i][x], D[i | (2 ^ x)][x]) + 1
其中 x 為節點 j 的鄰居(每一個都要算),而後者 (i | (2 ^ x)) 即代表著「探訪」該節點後的狀態、前者則是代表「經過」該節點(不改變狀態,即使該節點還沒探訪過)。
而停止條件就淺顯易懂,即是當 i 這個二進位數字全部都是 1 時,D[i][j] = 0。
又因為所有節點都可以當開頭,因此我們的所求最短路徑即是
min(D[2 ^ 0][0], D[2 ^ 1][1], ……, D[2 ^ (n - 1)][n - 1])
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。