題目連結(jié):
題目意譯:
給定兩個(gè)二元搜尋樹(Binary Search Tree,BST)root1 和 root2,回傳一個(gè)列表其包含著這兩棵樹中所有數(shù)字並按照升序排列。
限制:
每棵樹中的節(jié)點(diǎn)數(shù)位於範(fàn)圍 [0, 5000] 中。
-10 ^ 5 ≦ Node.val ≦ 10 ^ 5
範(fàn)例測(cè)資:
範(fàn)例 1:
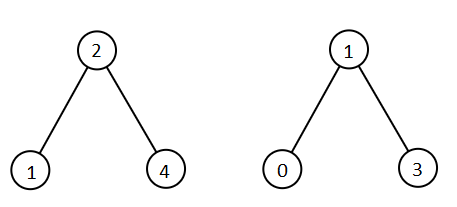
輸入: root1 = [2,1,4], root2 = [1,0,3]
輸出: [0,1,1,2,3,4]
範(fàn)例 2:
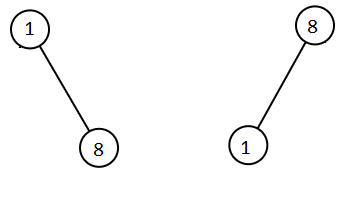
輸入: root1 = [1,null,8], root2 = [8,1]
輸出: [1,1,8,8]
解題思維:
(以下用 n 代稱兩棵樹的節(jié)點(diǎn)總數(shù))
除了把兩棵樹探訪過(guò)一次並將所有數(shù)字放到一個(gè)新的陣列後再排序,也就是 O(n log n) 的作法以外,還有一個(gè) O(n) 的作法——以前有提及過(guò) BST 的中序探訪(Inorder Traversal)是一個(gè)排序的數(shù)列(如
這題),再加上我們知道怎麼在線性時(shí)間內(nèi)合併兩個(gè)已排序之?dāng)?shù)列成為另一個(gè)已排序之?dāng)?shù)列(如這題)。因此,我們只需要兩次中序探訪加上線性的合併,便可以在 O(n) 之間把兩棵樹的數(shù)字合併成一個(gè)按升序排列的數(shù)列。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。