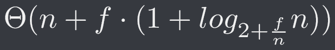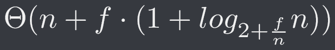題目連結:
題目大意:
輸入第一列給定兩正整數 n 、 q(n 、 q ≦ 5 × 10 ^ 6),代表現在有 n 個人依序站在位置 1 ~ n 上,並且有 q 筆的操作。
接著的 q 列輸入,每列先給定一個 '?' 或是 '-',並跟隨一個正整數 x(1 ≦ x ≦ n)。前者('?')代表我們要詢問位置 x 上往右(即往 x 、 x + 1 、 x + 2 等等的方向看去,注意記得 x 本身是有被包含的)第一個還存在的人之位置為何,如果右側沒有人就輸出 -1;而後者('-')則代表我們要把位置 x 的人移出隊伍之中。
請輸出每次 '?' 之詢問的結果。
(原作者注:「由於生測資的時候出現意外,每筆測資除了第一行以外每一行最後面都有一個空格。」)
時限:0.6s
測資量:> 50MB
範例輸入:
5 10
? 1
- 3
? 3
- 2
? 1
? 2
- 4
? 3
- 5
? 3
範例輸出:
1
4
1
4
5
-1
解題思維:
這題可以用併查集(Union-Find Set)解,不過不是一般常見的型態。因此下面就先介紹一下併查集這個資料結構。
任何資料結構只要滿足以下操作就可以叫做「併查集」:
建立(Make-set):顧名思義,建立一個新的集合,該集合包含一個作為參數傳入的元素 x。由於以下兩個操作的重要性較大,因此此操作通常會被某些人忽略不算在「必需」之內。
查詢(Find):查找一元素目前位於哪個集合之中。通常一個集合會有一個代表(Representative),可以用來判斷兩集合是否相同。
合併(Union):將兩個集合合而為一。
因為有合併以及查詢兩個操作,因故而稱為併查集(Union-Find set)。
而併查集常見的有兩種表示法,一種為連結串列(Linked List)、另一種為森林(Forest)。因為絕大部分的時候只會用到森林,因此以下只介紹森林的表示法:
下圖為一個有著兩棵樹的例子。
其中每棵樹代表一個集合,且 e 和 f 為各自的樹之根節點(root)以及「代表」。
可以看到在這樣的表示法之下,每個操作的時間複雜度為:
Make-Set(x):O(1),因為只是要建立一個新的節點而已。
Find(x):O(h),其中 h 為 x 所在的樹之高度,因為我們要從 x 循著邊跑到 root。
Union(x, y):O(h),因為要先找到 x 的根節點以及 y 的根節點,再將 x 的指向 y 的(反過來指也可以)。
而我們有兩種啟發式(Heuristic)可以最佳化上述操作時間複雜度的方式:
第一種為按秩合併(Union-by-rank),其代表的意思為在合併兩棵樹的時候把比較矮的(或是節點數少的)根節點指向比較高的(或是節點數多的)根節點。
因為矮的樹中的節點被詢問「代表」的比例比起高的樹中的節點還要來得低。因此在大部分情形下(或是以平均來看),高的樹節點多走了一層會比矮的樹節點多走一層還要虧。以上面的圖為例,把兩棵樹合併的話會是這樣:
第二種為路徑壓縮(Path Compression),即當每次呼叫為 Find(x) 找到 x 所在的樹之根節點 r 後,把 x 改成直接指向 r。承上例,當我們呼叫完 Find(c) 後,我們會得到:
呼叫為 Find(d) 後,我們會得到:
如果我們把上述兩種策略一起使用的話則就會變成一般我們常見到的併查集(Union-Find Set)之形式,其中均攤下(Amortized)單次 Find 和 Union 的操作之時間複雜度變為 α(n),其中 n 為全部元素的總數、α(n) 為反阿克曼函數(Inverse Ackermann Function),其函數值成長速度極慢(例如若 n = 2 ^ 2 ^ 2 …… ^ 2 之 k 層的指數塔,則 α(n) = k)。
有興趣探究為何是這樣的時間複雜度且英文程度尚可的讀者,可以考慮參見演算法的經典教科書——Introduction to Algorithms, Third Edition(或以四位作者的名字之開頭字母稱為 CLRS)裡的第 21 章。
實際上遇到需要併查集的問題時,實作森林的方式基本上不是真的用好幾個樹節點來表示,而是直接把所有東西攤平成若干個陣列來儲存。例如現在每個元素剛好是編號 1 ~ n,那麼我們就直接利用一個陣列 parents 來代表每個元素所指向的元素;而秩(rank)可以用另一個陣列來表示。
回到本題原先的目標——我們要找到從每個位置 x 開始往右第一個遇到有人在的位置(如果都沒有人,則為 -1)。正如一開始預告的,本題可以使用並查集解出。那麼要怎麼做呢?一樣,我們一開始有一個長度為 n + 2 的陣列 parents,其中 parents[i] 代表從位置 i 開始往右第一個有人的位置。
一開始對於所有 i = 1 ~ n 之值 parents[i] = i,因為每個位置都有站一個人。然後為了實作方便 parents[n + 1] = -1,代表再往右就沒有人了。因此,我們可以看到每個位置 x 所在的集合之「代表」,即為從 x 開始往右第一個有人的位置。
現在定義一個函式 Find(x),其可以找到 x 所在集合之「代表」。由於現在我們還沒套用任何最佳化的策略,所以我們的 Find 函式只有
while (parents[x] != x && parents[x] != -1)
++x;
return parents[x];
之內容,也就是相當暴力地去往右找第一個有人的位置。
那麼現在我們便可以把題目定義的兩種指令,'?' 以及 '-' 給實作出來。
因為 '?' 就是詢問本身,所以我們輸出 Find(x) 即可;而 '-' 是要移除位置 x 上的人,因此我們可以視為位置 x 所在的集合與位置 x + 1 所在的集合合併,因此 parents[x] = Find(x + 1),可以看到我們把原先併查集的 Union 操作藏在了這裡。
接著我們試著套用看看先前提到的兩種啟發式的最佳化策略,即按秩合併以及路徑壓縮。
首先可以看到我們所有位置 x 的「箭頭」都是指向右邊(也就是 x + 1 之方向)。而按秩合併是看兩者集合之高度或大小來決定合併方向,因此有可能會使箭頭往左指,而這不是我們樂見的結果。因此無法套用按秩合併。
接著是路徑壓縮,而這個策略是可以套用的。因此現在我們的 Find 函式會變得像是如下的結果:
第一部分是在找出「代表」,如下:
int index = x;
while (parents[index] != x && parents[index] != -1)
index = parents[index];
int result = parents[index];
第二部分是把路上經過所有位置的「代表」變成我們剛剛找到的「代表」,而這個行為即是路徑壓縮(Path Compression):
int buffer = x;
while (buffer < index) {
int temporary = parents[buffer];
parents[buffer] = result;
buffer = temporary;
}
return result;
而這樣便完成了我們的併查集最佳化。
那麼總體時間複雜度呢?可以看到我們有 n 個位置,所以有 n 個 O(1) 時間的 Make-Set 以及至多 n - 1 次的 Union,並假設我們總共呼叫 Find() 函式 f 次。由於我們的併查集只有使用路徑壓縮的策略,因此跟經常使用到的併查集不一樣,我們的時間(根據 CLRS)會是
也就是當 f 之值越大時,單次 Find() 平均所花的時間越少。
但是很不幸的是本題到這裡並還沒有結束,可以看到本題的測資量異常地大且時限非常地緊。所以我們需要使用如
這題中所使用的輸出入最佳化以及編譯器最佳化等等之手段。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。