題目連結:
題目意譯:
現在有 n 座城市編號為 0 到 n - 1 其中所有城市都有連接著一些雙向的道路。道路以一個二維整數陣列 edges 表示,其中 edges[i] = [xi, yi, timei] 代表著城市 xi 和 yi 之間需要花 timei 來往的一條道路。可能存在兩個相同的城市之間有著不同的往返時間,但是一座城市不會有道路連回到自己。
每次你經過一個城市,你必須付過路費。這將以一個索引值從 0 開始長度為 n 的整數陣列 passingFees 所表示,其中 passingFees[j] 代表當你經過城市 j 時需要付金額數。
一開始,你開始於城市 0 且想要在 maxTime 分鐘之內到達城市 n - 1。你旅程的費用為你於路途中經過的所有城市之過路費總和(包含開頭以及目標城市)
給定 maxTime 、 edges 和 passingFees,回傳要完成你的旅程最少所需的花費。如果無法在 maxTime 分鐘內完成則回傳 -1。
限制:
1 ≦ maxTime ≦ 1000
n == passingFees.length
2 ≦ n ≦ 1000
n - 1 ≦ edges.length ≦ 1000
0 ≦ xi 、 yi ≦ n - 1
1 ≦ timei ≦ 1000
1 ≦ passingFees[j] ≦ 1000
圖中的兩個節點之間可能包含多條邊。
圖不包含自環。
範例測資:
範例 1:
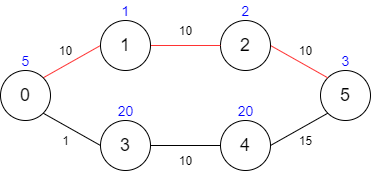
輸入: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
輸出: 11
解釋: 應走的路徑為 0 → 1 → 2 → 5,其將花費 30 分鐘以及 11 元的過路費。
範例 2:
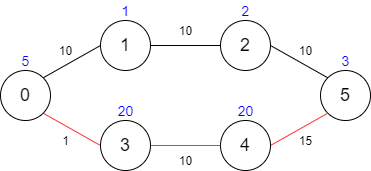
輸入: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
輸出: 48
解釋: 應走的路徑為 0 → 3 → 4 → 5,其將花費 26 分鐘以及 48 元的過路費。
你不能走 0 → 1 → 2 → 5 這條路徑,因為它會花太多時間。
範例 3:
輸入: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
輸出: -1
解釋: 沒有任何方式可以在 25 分鐘之內從城市 0 到城市 5。
解題思維:
首先把題目給定的 edges 轉成鄰接表(Adjacency List,如
這題),我們叫這個為陣列 P,其中 P[i] 儲存著城市 i 可以去到的城市之編號以及所耗時間。
接著我們可以利用動態規劃(Dynamic Programming)解出本題:
定義一個二維陣列 D,其中 D[t][i] 代表著在花費 t 分鐘的情況下到達第 i 座城市最少所需的過路費。則我們可以按照以下方式求出每對 (t, i) 之值:
D[0][0] = passingFees[0](因為無須花任何時間即可抵達城市 0);其他位置則先預設值為無窮大。
接著窮舉 t = 1 到 maxTime,而對於每個 t 值又再窮舉 i 值從 0 到 n - 1。對於每個 i 值我們逛過一次城市 i 可以前往的城市們,即 P[i]。當從城市 i 前往到某城市 j 要花 K 分鐘(記住從 j 到 i 也會是 K 分鐘)且 K < t 時,我們可以求得
D[t][i] = min(D[t][i], D[t - K][j] + passingFees[i])
也就是我們看在第 t - K 分鐘時從 j 出發到 i 是否有比現在還要好,更好的就更新成該值。因此,其實也可以寫成
D[t][j] = min(D[t][j], D[t - K][i] + passingFees[j])
兩者皆可。
上述窮舉過程結束後,最後再從 1 到 maxTime 窮舉一次 t 值,看當中 D[t][n - 1] 何者最小。如果每一個都是無限大,則代表著我們無法在 maxTime 之內從城市 0 跑到城市 n - 1,因此回傳 -1;反之回傳其中的最小值即為所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。