題目連結(jié):
題目意譯:
給定一個(gè)圓的半徑以及其圓心之位置,實(shí)作函式 randPoint 其將產(chǎn)生一個(gè)圓中的均勻(Uniform)隨機(jī)點(diǎn)。
實(shí)作類別 Solution:
Solution(double radius, double x_center, double y_center) 初始化一個(gè)物件,有著圓半徑 radius 以及圓心位置 (x_center, y_center) 。
randPoint() 回傳圓中的一個(gè)隨機(jī)的點(diǎn)。一個(gè)位於圓周上的點(diǎn)視為在圓內(nèi)。答案以陣列形式 [x, y] 回傳。
限制:
0 < radius ≦ 10 ^ 8
-10 ^ 7 ≦ x_center 、 y_center ≦ 10 ^ 7
最多有 3 × 10 ^ 4 次呼叫為 randPoint。
範(fàn)例測(cè)資:
輸入
["Solution", "randPoint", "randPoint", "randPoint"]
[[1.0, 0.0, 0.0], [], [], []]
輸出
[null, [-0.02493, -0.38077], [0.82314, 0.38945], [0.36572, 0.17248]]
解釋
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // 回傳 [-0.02493, -0.38077]
solution.randPoint(); // 回傳 [0.82314, 0.38945]
solution.randPoint(); // 回傳 [0.36572, 0.17248]
解題思維:
假設(shè) RAN 為一個(gè)介於 0 ~ 1 之間的隨機(jī)數(shù)(C++ 可能會(huì)寫(xiě) double(rand()) / RAND_MAX 來(lái)得到這樣的 R 值,python 則為 random.random())。
雖然你可以直接生成一個(gè)點(diǎn)為 (x_center + (2RAN - 1) × radius, y_center + (2RAN - 1) × radius) (2RAN - 1 代表著 -1 ~ 1 之間的一個(gè)隨機(jī)數(shù))然後判斷該點(diǎn)有沒(méi)有在圓內(nèi)。如果在就回傳該點(diǎn)座標(biāo);反之就繼續(xù)隨機(jī)產(chǎn)生另一個(gè)點(diǎn)直到在圓內(nèi)。
這樣依然可以確保圓內(nèi)的點(diǎn)有著均勻分布的機(jī)率會(huì)被選到,儘管看似有些點(diǎn)被拋棄了。但是因?yàn)檎w是均勻分布的,所以就算現(xiàn)在侷限範(fàn)圍於一圓仍是均勻分布。上述方法稱為棄卻抽樣(Rejection Sampling)。
但是這樣如果運(yùn)氣不好的話,有機(jī)會(huì)需要重複挑選相當(dāng)多次的點(diǎn)才會(huì)落在圓內(nèi),意即生成單一一個(gè)隨機(jī)點(diǎn)的最差時(shí)間複雜度為 O(∞)。
因此我們可以採(cǎi)取極座標(biāo)(Polar Coordinate)隨機(jī)取點(diǎn)——即標(biāo)準(zhǔn)座標(biāo)平面上的點(diǎn) (x, y) 會(huì)被改寫(xiě)為 (dcos(θ), dsin(θ)) ,其中 θ 為向量 (x, y) 與 X 軸之夾角 、 d 為 sqrt(x ^ 2 + y ^ 2),即點(diǎn) (x, y) 到原點(diǎn) (0, 0) 之距離。
所以我們可以改為隨機(jī)產(chǎn)生出兩個(gè)變數(shù)值 L = RAN × radius 、 A = RAN × 2π ,然後套入上面的極座標(biāo)格式便可以得到一點(diǎn) (x_center + Lcos(A), y_center + Lsin(A)) 。而此點(diǎn)保證在圓內(nèi),不需特別判斷。
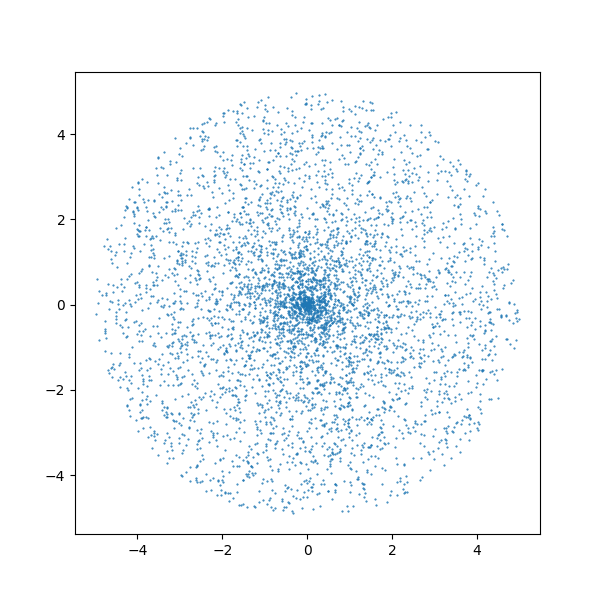
但是這樣會(huì)有一個(gè)大問(wèn)題,即現(xiàn)在點(diǎn)不再是均勻分布了(儘管看起來(lái)應(yīng)該要是均勻的)。如果我們真的按照上述方式取點(diǎn),我們會(huì)看到:
(上圖的取點(diǎn)數(shù)為 5000 個(gè))
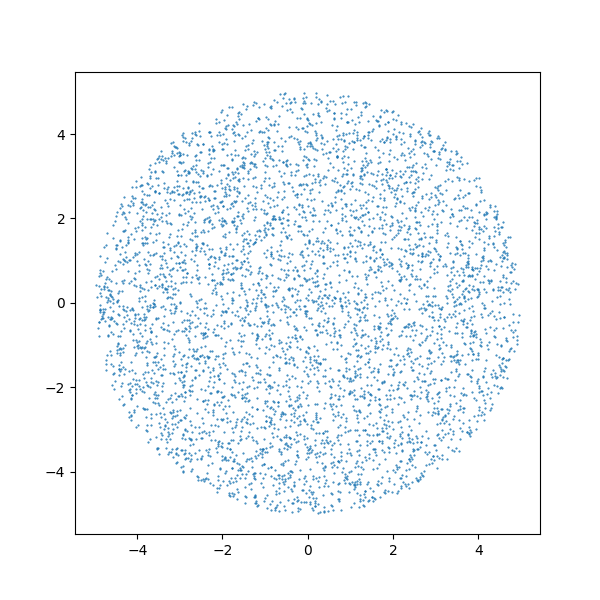
而將 L 的值改為 sqrt(RAN) × radius 即可以得到類似以下的均勻分布:
(取點(diǎn)數(shù)同樣是 5000 個(gè)點(diǎn))
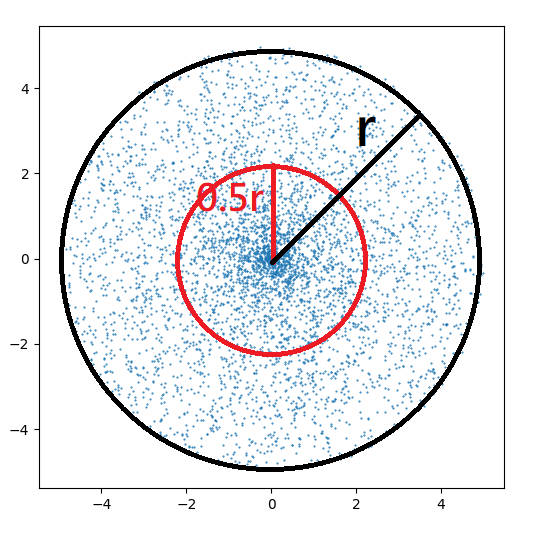
原因可以從下圖看出:
可以看到,原本 L 之值落在 [0, r] 或是 [r, 2r] 這兩個(gè)範(fàn)圍是均等的,而角度 θ 從 0 度 ~ 360 度(或是弧度 0 ~ 2π)也是均等的機(jī)率。
但是圖中兩個(gè)同心圓,中間的圓因面積為較小所以只需要較少的點(diǎn)便可以填滿(也就是點(diǎn)密度會(huì)較大);相對(duì)的較外層的圓,因?yàn)槊娣e大,所以需要較多的點(diǎn)填滿(也就是點(diǎn)密度會(huì)較小)。而密度差便造成了機(jī)率分布的不均勻(機(jī)率的「本質(zhì)」與密度有著密切關(guān)係)。
而密度與距離圓心的距離 r ^ 2 成正比。因此當(dāng)我們將 RAN 取 sqrt() (即取其平方根),我們便可以抵銷掉 r ^ 2 所帶來(lái)的密度差(因?yàn)?0 ~ 1 之間的數(shù)字取平方根後會(huì)更靠近 1,例如 sqrt(0.25) = 0.5)。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說(shuō)明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。