題目連結:
題目意譯:
給定一個矩陣 matrix 以及一個目標整數 target,回傳總和為 target 的非空子矩陣之數量。
一個子矩陣 (x1, y1, x2, y2) 為所有格子 matrix[x][y] 之集合,其中 x1 ≦ x ≦ x2 且 y1 ≦ y ≦ y2。
兩個子矩陣 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 視為不同子矩陣,如果它們有一些座標值不一樣:例如 x1 ≠ x1' 等。
限制:
1 ≦ matrix.length ≦ 100
1 ≦ matrix[0].length ≦ 100
-1000 ≦ matrix[i] ≦ 1000
-10 ^ 8 ≦ target ≦ 10 ^ 8
範例測資:
範例 1:
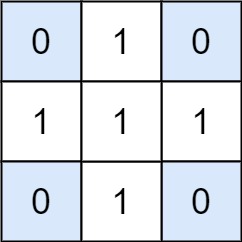
輸入: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
輸出: 4
解釋: 答案為那四塊 1 × 1 只包含著 0 的子矩陣。
範例 2:
輸入: matrix = [[1,-1],[-1,1]], target = 0
輸出: 5
解釋: 兩個 1 × 2 子矩陣,加上兩個 2 × 1 子矩陣以及一個 2 × 2 子矩陣。
範例 3:
輸入: matrix = [[904]], target = 0
輸出: 0
解題思維:
假設給定的矩陣有 r 列 c 行。
先將矩陣中同一行的數字視為一個獨立的數列,然後對該數列計算其前綴和(Prefix Sum,參見
這題)。所以如果一個 r 列 c 行的矩陣將有 c 個前綴和。
因此如果矩陣是
0 1 0
1 1 1
0 1 0
其前綴和矩陣 P 可能為
0 0 0
0 1 0
1 2 1
0 3 0
最上面多了一列 0 是因為計算時的方便性。例如要求第 C 行從第 L ~ R 列(L ≦ R)之總和可以寫為 P[R + 1][C] - P[L][C]。沒有最上面一排 0,會需要額外判斷 L 是否為 0。
接著我們窮舉 (i, j) 數對,其中 0 ≦ i ≦ j < r,代表著我們現在要窮舉每種可能的子矩陣之上下緣(也就是代表著從第 i 列開始到第 j 列結束的子矩陣)。
對於每個 (i, j) 我們用另一索引值 k 代表著當前行數,用來計算 (P[j + 1][0] - P[i][0]) ~ (P[j + 1][k] - P[i][k]) 之值。而這個步驟可以再套用一次前綴和。例如沿用上面的範例:
原矩陣為
0 1 0
1 1 1
0 1 0
其前綴和矩陣 P 為
0 0 0
0 1 0
1 2 1
0 3 0
而我們現在是要求第 0 列 ~ 第 1 列的子矩陣,此時定義一變數 S = 0 代表總和。而上述的步驟會得到
0 0 0
0 1 0
1 2 1
0 3 0
S += P[2][0] - P[0][0]
S = 1
0 0 0
0 1 0
1 2 1
0 3 0
S += P[2][1] - P[0][1]
S = 4
0 0 0
0 1 0
1 2 1
0 3 0
S += P[2][2] - P[0][2]
S = 5
在更新 S 前,我們建立一個雜湊表 H(Hash Table)用以統計每一種總和出現的次數,因此 H[S] 就代表著有多少固定從第 i 列 ~ 第 j 列、第 0 行開始的子矩陣總和為 S(也就是固定了子矩陣的上下側以及左側,被窮舉的是右側)。
基於計算方便性(如同前面的前綴和),我們將 H[0] 初始化為 1。
接著當我們每次更新完 S 後,我們計算 D = S - target 之值,然後去 H 中找尋 D 是否存在。
倘若 D 存在,代表先前可能有多個 k' 值(k' < k)其總和為 D ,因此我們可以仿照一般前綴和求區間總和的概念得到一個子矩陣
(i, j, k' + 1, k)
其總和為
(P[j+1][k'+1] - P[i][k'+1]) ~ (P[j+1][k] - P[i][k])
並且其值恰好為 target(即 S - D)。
而這樣的子矩陣有 H[D] 個。
計算後,記得將 H[S] 加 1 以示此時總和 S 之值出現次數 + 1。
而所求就是上述窮舉所有 (i, j) 過程中,期間所有 H[D] 之值的總和。時間複雜度為 r ^ 2 × c
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。