題目連結:
題目意譯:
我們有 n 個籌碼,其中第 i 個籌碼的位置為 position[i]。
我們需要移動所有的籌碼到同一個位置。在一個步驟中,我們可以改變第 i 個籌碼的位置 position[i] 為:
position[i] + 2 或 position[i] - 2 伴隨著成本 = 0。
position[i] + 1 或 position[i] - 1 伴隨著成本 = 1。
回傳將所有籌碼移動到同一位置的最小所需成本。
限制:
1 ≦ position.length ≦ 100
1 ≦ position[i] ≦ 10 ^ 9
範例測資:
範例 1:
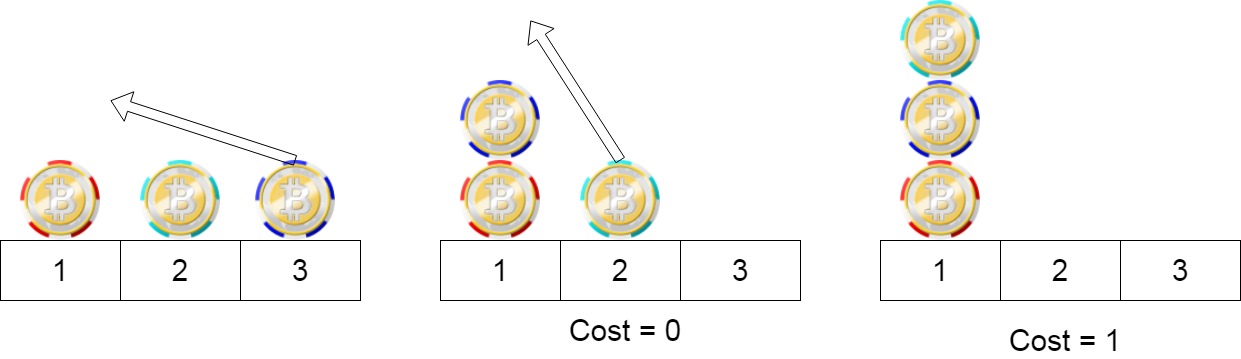
輸入: position = [1,2,3]
輸出: 1
解釋: 第一步: 移動在位置 3 的籌碼到位置 1 ,其成本 = 0。
第二步:移動位置 2 的籌碼到位置 1,其成本 = 1。
總成本為 1。
範例 2:
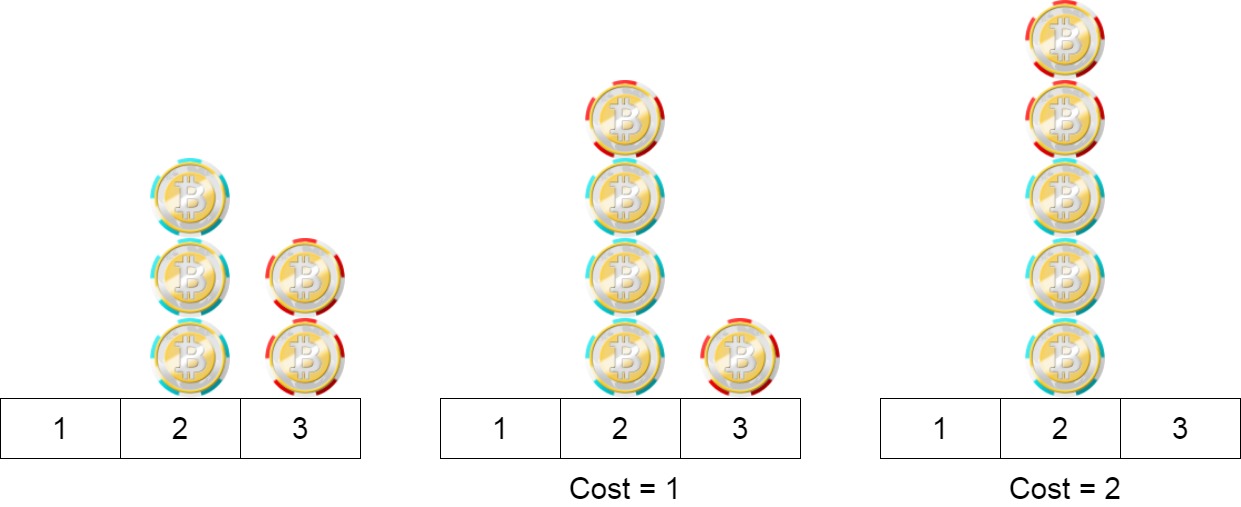
輸入: position = [2,2,2,3,3]
輸出: 2
解釋: 我們可以移動在位置 3 的兩個籌碼到位置 2。每個移動有著成本 = 1。總成本 = 2。
範例 3:
輸入: position = [1,1000000000]
輸出: 1
解題思維:
可以看到,當一個籌碼移動到與原本位置之奇偶性的位置時,成本為 0、移動到奇偶性不同的位置時,成本為 1。
而因為成本要儘可能地小,所以每個籌碼的位置之奇偶性最多應只改變一次。否則要是改變了超過一次,且最終位置的奇偶性與原本位置相同,那完全不更改奇偶性直接藉由「position[i] + 2 或 position[i] - 2」之操作的成本會更低;同樣地,如果目標位置奇偶性原本的位置不一樣,則可以先藉由「一個」「position[i] + 1 或 position[i] - 1」之操作來使得現在位置奇偶性與目標相同,最後再由若干個「position[i] + 2 或 position[i] - 2」操作來抵達目標。
而因為最後所有籌碼會抵達同一個位置,所以最後所有籌碼的位置之奇偶性皆相同。因此,要嘛是所有的奇數位置的籌碼跑到偶數位置、要嘛是所有的偶數位置籌碼跑到奇數位置。假設奇數位置的籌碼有 O 個、偶數位置的有 E 個,則最小成本為 O 和 E 中最小的,即
min(O, E)
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。