題目連結(jié):
題目大意:
現(xiàn)在有一機(jī)器人在一個(gè)全白的平面上的原點(diǎn)(0, 0)格子並面向上方(+y 方向)。每當(dāng)機(jī)器人在白色格子上,該格會(huì)變成黑色,而機(jī)器人會(huì)先向右轉(zhuǎn) 90° 然後往前走一格;如果機(jī)器人在黑色格子上,該格會(huì)變白,而機(jī)器人會(huì)向左轉(zhuǎn) 90° 然走一格。
輸入有多列,每列給定一正整數(shù) n (1 ≦ n ≦ 2 ^ 48),試問機(jī)器人走 n 步之後抵達(dá)的格子之座標(biāo)為何?
範(fàn)例輸入:
1
2
3
5
10
100
1000
2147483647
2147483648
2200000000
範(fàn)例輸出:
(1,0)
(1,-1)
(0,-1)
(-1,0)
(-1,-1)
(0,2)
(8,6)
(-41297588,-41297561)
(-41297588,-41297562)
(-42307516,-42307490)
解題思維:
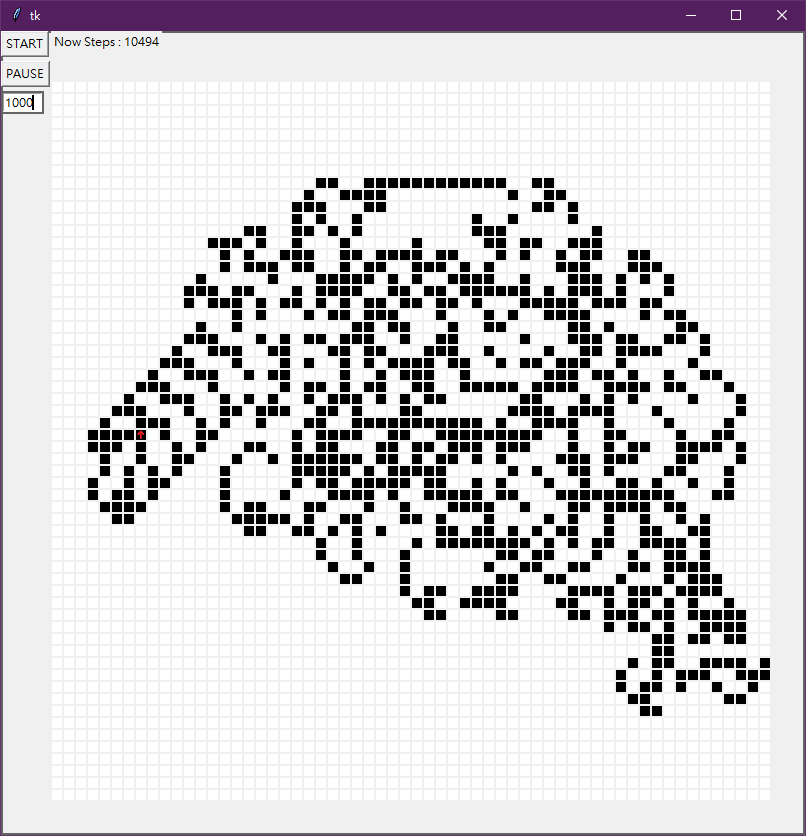
如果只是單純地模擬並輸出機(jī)器人的座標(biāo),可能看不出什麼所以然。但是如果我們以圖象將格子座標(biāo)視覺化,如下圖:
畫面的左中有個(gè)小紅色箭頭,代表機(jī)器人的位置以及面向的方向。上面有個(gè)「Now Steps:10494」,代表機(jī)器人從一開始到這個(gè)畫面為止走了 10494 步(至於左邊的數(shù)字只是調(diào)整機(jī)器人的執(zhí)行速度)。
可以看到畫面左方中間有個(gè)往左下伸出的結(jié)構(gòu),如果版面再開大一點(diǎn)並讓它繼續(xù)的話,是真的會(huì)一直往左下走的。因?yàn)閺拇蠹s 10200 步左右,開始會(huì)有重複、循環(huán)出現(xiàn)的模式(格子和機(jī)器人的方向),使得機(jī)器人會(huì)陷入一個(gè)無窮無盡的循環(huán)(每個(gè)循環(huán)為 104 步)之中。
事實(shí)上,這個(gè)機(jī)器人在數(shù)學(xué)上被稱為「蘭頓螞蟻」(Langton's Ant,見
維基頁面之介紹),因?yàn)樘岢稣呤强死锼苟喾颍m頓(Christopher Langton)且是以螞蟻來充當(dāng)這題機(jī)器人所扮演的角色。
由上我們可以看到,將前 10500 步機(jī)器人的位置窮舉出來,剩下跑一次 104 步的循環(huán)並記錄每一步的位移、以及 104 的總位移(位移有 x 、 y 座標(biāo)的分量,要各自儲(chǔ)存)。
接著對(duì)於每個(gè)給定的步數(shù) n 值,判斷是否 ≦ 10500 (即窮舉出來的步數(shù))。如果是,就輸出對(duì)應(yīng)的窮舉出的該步之位置;如果不是就是第 10500 步的位置加上剩下 (n - 10500) ÷ 104 取商數(shù)(代表經(jīng)歷幾個(gè)循環(huán)) × 一個(gè)循環(huán)的總位移,最後再加上 (n - 10500) ÷ 104 的餘數(shù)(代表最末尾的循環(huán))的剩餘位移量,即是所求。
此次分享到此為止,如有任何更加簡(jiǎn)潔的想法或是有說明不清楚之地方,也煩請(qǐng)各位大大撥冗討論。