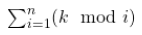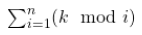主題
題目連結(jié)：
題目大意：
輸入有多列，每列給定兩正整數(shù) n 、 k （1 ≦ n 、 k ≦ 10 ^ 9），求下式之值
範(fàn)例輸入：
5 3
範(fàn)例輸出：
7
解題思維：
先不管 n ，只看 k 在不同的 i 值之下其餘數(shù)為何。
可想而知，當(dāng) i > k 時， k mod i 的值全都是等於 k 。所以我們也先忽略 i > k 的情形。此時觀察較小的 k 值（1 ～ 10 那種）可能看不出什麼所以然。因此，我們來看看以下 k ＝ 144 的情況：
可以看到，最左邊的那個直行代表著不同的 i 值，右邊兩個分別是 k 除以 i 之後的商數(shù)以及餘數(shù)。
前面可能看不出特別的樣子。但是到了中段的部分可以開始看到 k % i 那一行的數(shù)字開始形成一群一群的等差數(shù)列。而這些數(shù)列裡面的所有數(shù)字，其 k / i 那行的值皆是一樣的，且 k / i 正是其數(shù)列之公差（只是是負(fù)的）。
因此，我們可以靠上面觀察到的性質(zhì)來加速遍歷 i 值的過程。當(dāng)遇到一個 i 值時，先計算 k / i 之商數(shù) q 以及餘數(shù) r 。然後計算 k / q 取其商 t，而該數(shù)則是會與現(xiàn)在 i 值得到一樣 k / i 之商數(shù)的最大值。也就是說我們找到了一個上面觀察到的等差數(shù)列之開頭與結(jié)尾。
而套入等差級數(shù)的公式（假設(shè)項數(shù)有 m 項，m ＝ t - i + 1），我們可以得到這段的 (k mod i) + (k mod (i + 1)) +…… + (k mod t) 之值為
(2r - q × (m - 1)) × m ÷ 2
最後將 i 值更新為 t + 1 。重複直到 i > k 。
而上述的過程從 i ＝ 1 開始，即可完整覆蓋到所有的等差數(shù)列。但是因為我們不是要求
(k mod 1) + (k mod 2) + …… + (k mod k)
而是要求
(k mod 1) + (k mod 2) + …… + (k mod n)
所以遍歷的過程中，當(dāng) t 一旦大於 n （此時代表 n < k），則將 t 值限縮到等於 n （畢竟只求到 n）。而遍歷過程的中止條件除了原本的 i 大於 k ，還要加上 i 等於 n + 1 的時候也要跳出（因為 t 如果等於 n ，i 值將被更新成 n + 1）。
剩下的情況是，結(jié)束過程後的 i 值如果小於等於 n。則計算結(jié)果還要加上
(n - i + 1) × k
因為 (k mod (k + 1)) 、 (k mod (k + 2)) 、(k mod (k + 3)) 等等的值皆為 k 。
上述都跑完、判斷完之後，最終的總和即是所求。
此次分享到此為止，如有任何更加簡潔的想法或是有說明不清楚之地方，也煩請各位大大撥冗討論。
達(dá)人
