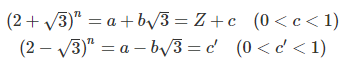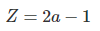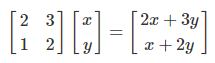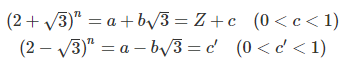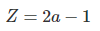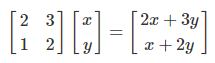題目連結：
題目大意：
給定一正整數 ｎ （ ０ ≦ ｎ ≦ ２, ０００, ０００, ０００ ），求（２＋√３） ^ ｎ 的整數部分之末三位。若不足三位長，請補足前導 ０ 。
範例輸入：
0
1
2
3
10
123456789
範例輸出：
001
003
013
051
173
451
解題思維：
關於這題有個不錯的性質：設（２ ＋ √３） ^ ｎ ＝ ａ ＋ ｂ√３ （ａ、ｂ ∈ ? ），則 （２ ＋ √３） ^ ｎ 之整數部分便為 ２ａ － １ 。
以下為證明：
我們可以假設以下兩式，而一式中的 Ｚ 即是題目想要求的整數部分
再將兩式相加，得到
而因為等號左邊為一正整數，因此右邊也為一正整數。且因 ０ ＜ ｃ、ｃ’ ＜ １，所以 ｃ ＋ ｃ’ 必等於 １ （ Ｚ 本來已經就是正整數）。於是
得證。
有了以上的背景知識後，那要怎麼快速得到 ａ ＋ ｂ√３ 中的 ａ 呢？觀察以下關係式：
已知（２ ＋ √３） ^ ｎ ＝ ｘ＋ｙ√３
則（２ ＋ √３） ^ （ｎ ＋ １） ＝ （２ｘ＋３ｙ） ＋ （ｘ＋２ｙ）√３
轉成矩陣相乘的形式即為：
設以上的 ｘ ＝ １ 、 ｙ ＝ ０，在左邊乘一個上式最左邊的矩陣（以下稱矩陣 Ａ ）得到２ ＋ √３）；再乘一個 Ａ ，得到 ７＋４√３；乘 ｎ 個 Ａ ，得到（２ ＋ √３） ^ ｎ 。
然後，再套用矩陣快速冪的概念（本人的這篇文章有提到），並在相乘的時候取 １, ０００ 的餘數。這樣便可快速得到（２ ＋ √３） ^ ｎ ＝ ａ ＋ ｂ√３ 中的 ａ、ｂ 。
最後，算出 ２ａ － １ 之後，再取 １, ０００ 的餘數即是所求。（注意數字的長度，可能不足三位長，這時要在前面補 ０ ）
此次分享到此為止，如有任何更加簡潔的想法或是有說明不清楚之地方，也煩請各位大大撥冗討論。
達人