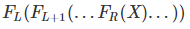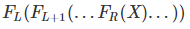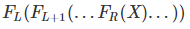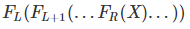題目連結：
題目大意：
給定兩正整數 Ｎ （ １ ≦ Ｎ ≦ ２００, ０００ ）、 Ｑ （ １ ≦ Ｑ ≦ ２００, ０００ ）。表示一開始有Ｎ個函數，且全部都是遞增的函數。像是Ｆ（Ｘ），當Ｘ越大，Ｆ（Ｘ）之值越大，則Ｆ（Ｘ）就是一個遞增的函數；反之，則是一個遞減函數。
而現有 Ｑ 行，每行第一個數字為 Ｖ 。
如果 Ｖ ＝ １ ，則接下來有一正整數 ｉ ，代表第 ｉ 個函數的增減性要反過來（增函數變成減函數、減函數變增函數）。
若 Ｖ ＝ ２ ，則會接著兩正整數 Ｌ 、 Ｒ （ １ ≦ Ｌ ≦ Ｒ ≦ Ｎ ），求：
上述值的增減性（也就是把上述式子看作一個新函數），其中 ＦＬ 代表第 Ｌ 個函數，以此類推。遞增則輸出「0」；反之，輸出「1」。
範例輸入：
5 3
2 2 4
1 3
2 2 4
範例輸出：
0
1
解題思維：
首先，我們觀察只有 ３ 個函數的時候：
一開始都是增函數，所以 Ｆ１（Ｆ２（Ｆ３（Ｘ））） 當然也是增函數。
而現在我們把第２個函數翻轉增減性，因此 Ｆ２（Ｆ３（Ｘ）） 變成了一個遞減函數，所以 Ｆ１（Ｆ２（Ｆ３（Ｘ））） 也變成了一個遞減函數。
而再把第３個函數翻轉，因此 Ｆ２（Ｆ３（Ｘ）） 變回了一個遞增函數，而 Ｆ１（Ｆ２（Ｆ３（Ｘ））） 也變回了增函數。
以上我們可以發現：如果把增函數當作１，減函數當作－１。則
的增減性即為各個函數增減性所代表的數字之乘積。像是上面的例子， Ｆ１（Ｆ２（Ｆ３（Ｘ））） 之增減性 ＝ １* （－１） * （－１）＝ １ ，因此是遞增的函數。
但是因為 Ｎ 、 Ｑ 可以高達 ２００, ０００ ，而如果我們每次詢問增減性的時候就要用迴圈去跑一次乘積，最糟的時間複雜度為 Ｏ（ＮＱ） ，然而時間限制為 １ 秒。
就算使用前綴預處理的概念，在更新函數的增減性之時，最糟要從 １ 跑到 Ｎ 。因此最糟的時間複雜度仍然是 Ｏ（ＮＱ） 。
因此，我們又要像 d712: The 3n + 1 problem 這題一般去使用「偽線段樹」。只是這次節點儲存的是區間的增減性、更新時也是更新增減性而已。如此一來，便可以在時間範圍內達到所需，時間複雜度為 Ｏ（Ｑ * ｌｏｇＮ）。
